Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 19.2 - Ex. 15
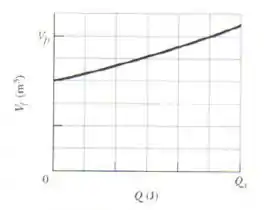
Suponha que de um gás ideal sofra uma expansão isotérmica quando uma energia é acrescentada ao gás na forma de calor. Se a figura mostra o volume final em função de , qual é a temperatura do gás? A escala do eixo vertical é definida por e a escala do eixo horizontal é definida por .
Passo 1
Falaaa galerildis, tudo bem com vocês?!
Saca só, aqui a gente sabe que o processo é isotérmico, então a gente pode tirar que:
Beleza. Isso é útil porque calcular o trabalho é mais fácil do que calcular o calor. No processo isotérmico, a fórmula pra calcular o trabalho é essa aqui:
E então teremos:
Passo 2
Agora é só dar uma olhada no gráfico. Ele diz, por exemplo, que quando o volume varia de:
Para:
A quantidade total de calor acrescentado foi:
Isso porque cada “traço” no eixo vertical vale , e cada traço no eixo horizontal vale .
Passo 3
Então vamos substituir esses valores na equação.
Pronto!
Resposta
A temperatura é .