Suponha que o trenó do Exercício 6.24 esteja inicialmente em repouso em x= 0. Use o teorema do trabalho-energia para achar velocidade a do trenó em a) x= 8,0 m; b) x = 12,0 m. Despreze o atrito entre o trenó e a superfície do lago.
Passo 1
Fala aí, pessoal! Nessa questão primeiro temos que relembrar os dados do trenó do Exercício 6.24.
É um trenó de massa 10,0 kg sob a aplicação de uma força descrita pelo seguinte gráfico:
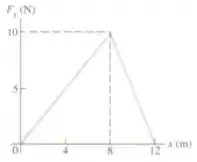
Passo 2
Beleza? Agora podemos começar a aplicar o teorema trabalho-energia neste problema.
Como a única energia envolvida nesse caso é a Energia Cinética. Teremos:
Substituindo a massa do trenó na equação:
Passo 3
Então, agora só precisamos substituir com os valores obtidos no Exercício 6.24!
Partindo do repouso, nós obtivemos que quando o trenó chegou à .
Como ele parte do repouso, .
Neste caso a velocidade final dele será a velocidade quando .
Para não é diferente! Novamente partindo do repouso, nós obtivemos que quando o trenó chegou à .
Como ele parte do repouso, .
Resposta
- m/s
- m/s