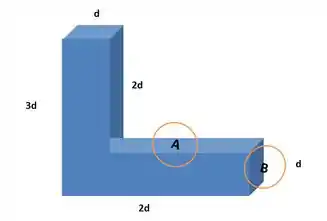
O tanque em forma de mostrado na Figura está cheio d’água e é aberto na parte de cima. Se , qual é a força exercida pela água: (a) Na face e (b) Na face ?

Agora na face B temos que tomar mais cuidado. Isso por que a força não é constante, já que a superfície é vertical. Pra isso vamos dividir a superfície em vários retângulos de base e altura , então cada retângulo desses terá uma área . A força em cada partezinha será dada como:

Como é a área de uma retângulo de base e altura :

Então temos que:

Dessa forma, a pressão na base da face B será igual a:

E no topo da base B:

Repare que, conforme aumentamos a altura, menor será a pressão. Então, ao longo da base B a pressão em um ponto a uma altura da base é dada como:

Dessa forma:

Belezoca, agora como temos apenas uma força , para encontrarmos a força total exercida, vamos integrar a força de até , assim:

Resolvendo a integral, obtemos que:

Colocando em evidência:

Substituindo os valores: