Duas esferas de são mantidas fixas em um eixo , uma em e a outra em . Uma bola de é liberada a partir do repouso em um ponto do eixo que está a uma grande distância (praticamente infinita) das esferas. Se as únicas forças que agem sobre a bola são as forças gravitacionais exercidas pelas esferas, então, quando a bola chega ao ponto , quais são (a) a energia cinética da bola e (b) a força resultante exercida pelas esferas sobre a bola, em termos dos vetores unitários?
Passo 1
Vamos começar desenhando a situação em um plano cartesiano:
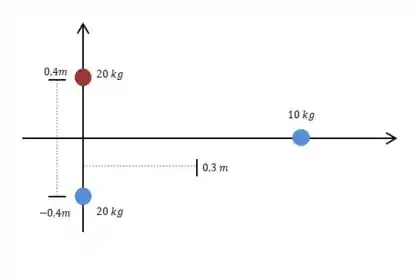
A letra (a) quer saber qual vai ser a energia cinética da bola quando ela chegar no ponto de coordenadas .
Para descobrir isso, vamos usar a lei de conservação de energia.
Passo 2
Inicialmente, a bola de massa estava em repouso (portanto ), e a uma distância “praticamente infinita” (portanto ). Portanto a energia mecânica inicial é:
Quando estiver no ponto de coordenadas , a energia mecânica vai ser:
Então falta achar as energias potenciais gravitacionais entre a bola de massa e cada uma das outras duas.
Pela figura podemos ver que a distância entre os pares é a mesma. Vamos calculá-la usando o teorema de Pitágoras:
E substituindo na fórmula da energia potencial gravitacional:
Passo 3
Agora voltando à lei de conservação de energia:
O substituindo o valor que acabamos de encontrar:
Pronto, essa é a resposta da letra (a).
Passo 4
Para calcular a força resultante naquele ponto, temos primeiro que calcular o módulo das forças entre a bola de e cada uma das outras duas.
Perceba que as duas forças são iguais em módulos, pois as massas e as distâncias são iguais:
Esse é o comprimento do vetor desenhado abaixo, assim como do outro (seu reflexo no eixo ) que representa a força com a bala mais abaixo:
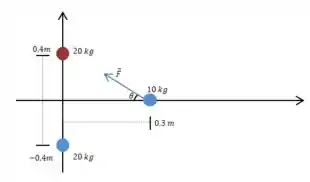
Passo 5
Perceba que as duas forças se cancelam no eixo , e se somam no eixo . Por isso a força resultante terá apenas um componente no eixo , apontando para a origem.
Vamos calcular esse componente:
Como as forças se somam, o módulo da resultante será:
Que como vimos, aponta no sentido negativo do eixo :
Resposta
(a)
(b)