Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 7.3 - Ex. 26

Um trabalhador d e   75   k g sobe por uma escada de 7,0   m até o telhado plano de uma casa. Ele caminha 12   m sobre o telhado, desce por outra escada vertical de 7,0   m e finalmente caminha

pelo solo de volta ao seu ponto de partida. Quanto trabalho a gravidade realiza sobre ele (a) enquanto ele sobe; (b) enquanto ele desce; (c) enquanto ele caminha sobre o telhado e sobre o solo? (d) Qual é o trabalho total realizado sobre ele pela gravidade no percurso completo? (e) Com base na resposta do item (d), você afirmaria que a gravidade é uma força conservativa ou não conservativa? Explique.

Passo 1

Oi, galerinha! Tudo bom? Vamos começar descrevendo esse movimento. Sendo A o ponto inicial, o que ele tá fazendo é isso.

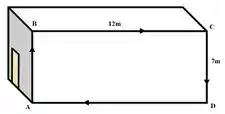
O trabalho de uma força será sempre:

W = F ∙ ∆ S ∙ cos ⁡ ϕ

Onde:

  • F Força em questão
  • ∆ S Deslocamento
  • ϕ Ângulo entre a força aplicada e o deslocamento.

Como a única força é a força peso, temos:

F = P = m g

E logo:

W G = m g ∆ S cos ⁡ ϕ

Agora pra calcular o trabalho em cada parte do movimento, vamos dividir em: movimentos verticais e movimentos horizontais!

Passo 2

Vamos começar com os movimentos verticais, ou seja, a subida e a descida. Dá só uma olhada:

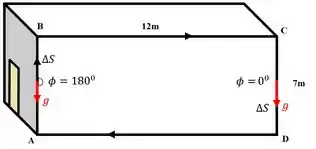
Os trabalhos serão:

Na subida (repara que o deslocamento é contrario a força da gravidade, logo o ângulo será de 180 ° )

W G A → B = m g ∆ S cos ⁡ 180 o

Substituindo os valores, sendo, do enunciado e da física:

  • m = 75   k g
  • g ≅ 9,81 m s 2
  • ∆ S = 7   m

Ficamos com,

W G A → B = 75   k g 9,81 m s 2 7   m - 1

W G A → B = 5150,25   N × m ‬

Na descida (repara que o deslocamento está a favor da força da gravidade, logo o ângulo será de 0 ° )

W G C → D = m g ∆ S cos ⁡ 0 o

Substituindo os valores,

W G C → D = 75   k g 9,81 m s 2 7   m 1

W G C → D = 5150,25   N × m

Passo 3

Agora pros movimentos horizontais, vamos ter:

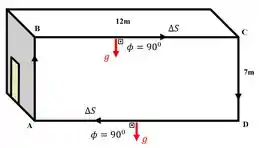
Em ambos os sentidos temos um ângulo de 90 ° com a força da gravidade, logo os serão:

W G B → C = m g ∆ S cos ⁡ 90 o

W G D → A = m g ∆ S cos ⁡ 90 o

Como, cos ⁡ 90 o = 0 .

Os trabalhos serão

W G B → C = 0   N × m ‬

W G D → A = 0   N × m

Passo 4

Bora calcular o trabalho total? Ele será:

W G T o t = W G A → B + W G B → C + W G C → D + W G D → A

W G T o t = - 5150,25 + 0 + 5150,25 + 0

W G T o t = 0   N × m

Ih, olha lá! Zerou! E galera, isso aí é o suficiente pra gente afirmar já que a gravidade é uma força conservativa. Afinal, o trabalho total realizado para uma viagem de ida e volta ao mesmo ponto é zero.

Resposta

  1. W G A → B = - 5150,25   N × m ‬
  2. W G C → D = 5150,25   N × m ‬
  3. W G B → C = 0   N × m W G D → A = 0   N × m
  4. W G T o t = 0   N × m
  5. O trabalho total realizado para uma viagem de ida e volta ao mesmo ponto é zero, indicando que a força é, de fato, conservativa
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Jane, com massa de 50,0k g , precisa se balançar para o outro lado de um rio (de largura D ), cheio de crocodilos devoradores de humanos, para salvar Tarzan do perigo. Ela tem de se balançar, na prese
Um bloco de 10,0k g é liberado do repouso no ponto A da Figura P7.71. A pista não tem atrito, com exceção da porção entre os pontos B e C, que tem comprimento de 6,00m . O bloco vai pista abaixo, bate
Em 1887, em Bridgeport, Connecticut, C. J. Belknap construiu um tobogã aquático mostrado na Figura P7.77. Um passageiro em um pequeno trenó, de massa total de 80,0k g , empurrou-se para começar no top
Considere a arma de brinquedo do Exemplo 7.3. Suponha que a massa do projétil, distância de compressão e constante da mola permaneçam as mesmas dadas ou calculadas no exemplo. No entanto, suponha, ain
29 . Uma esquiadora de 62k g está se movendo a 6,50m / s sobre um platô horizontal, sem atrito, coberto de neve, quando encontra um trecho áspero com 4,20m de extensão. O coeficiente de atrito cinétic