Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 7.Problemas - Ex. 81

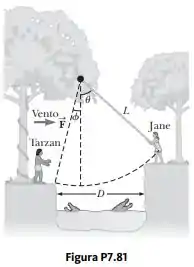
Jane, com massa de 50,0   k g , precisa se balançar para o outro lado de um rio (de largura D ), cheio de crocodilos devoradores de humanos, para salvar Tarzan do perigo. Ela tem de se balançar, na presença de um vento que exerce força horizontal constante  F → , em um cipó de comprimento L e fazendo um ângulo q com a vertical inicialmente (Fig. P7.81). Considere D   =   50,0   m , F   =   110   N , L   =   40,0   m e θ   =   50,0 º . (a) Com que velocidade mínima Jane deve começar seu balanço para conseguir chegar ao outro lado? (b) Depois do resgate completo, Tarzan e Jane têm de se balançar de volta para cruzar o rio. Com que velocidade mínima eles têm de começar seu balanço? Suponha que Tarzan tenha massa de 80,0   k g .

Passo 1

E aiii gente, tudo bem com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo!

A geometria mostra que D = L s i n ⁡ θ + L s i n ⁡ ϕ :

50.0 m = 40.0 m sin ⁡ 50 ∘ + sin ⁡ ϕ , ϕ = 28.9 ∘

Letra a:

Do começo ao fim o sistema Jane-Terra tem a seguinte velocidade mínima inicial:

Δ K + Δ U + Δ E int  = 0 0 - 1 2 m v i 2 + [ m g ( - L c o s ⁡ ϕ ) - m g ( - L c o s ⁡ θ ) ] + F D = 0 1 2 m v i 2 + m g ( - L c o s ⁡ θ ) + F D ( - 1 ) = 0 + m g ( - L c o s ⁡ ϕ )

1 2 50.0 k g v i 2 + 50.0 k g 9.80 m s 2 - 40.0 m cos ⁡ 50 ∘ - 110 N 50.0 m

= 50.0 k g 9.80 m s 2 - 40.0 m cos ⁡ 28.9 ∘

1 2 ( 50.0 k g ) v i 2 - 1.26 × 10 4 J - 5.5 × 10 3 J = - 1.72 × 10 4 J v i = 2 947 J 50.0 k g = 6.15 m s

Passo 2

Letra b:

Para o balanço de volta:

Δ K + Δ U = Δ E mec ânica   0 - 1 2 m v i 2 + m g - Lcos ⁡ θ - m g - Lcos ⁡ ϕ = F D 1 2 m v i 2 + m g - Lcos ⁡ ϕ + F D + 1 = 0 + m g - Lcos ⁡ θ

1 2 130 k g v i 2 + 130 k g 9.80 m s 2 - 40.0 m cos ⁡ 28.9 ∘ + 110 N 50.0 m

= 130 k g 9.80 m s 2 - 40.0 m cos ⁡ 50 ∘

1 2 ( 130 k g ) v i 2 - 4.46 × 10 4 J + 5500 J = - 3.28 × 10 4 J v i = 2 6340 J 130 k g = 9.87 m s

Resposta

  1. 6.15 m s
  2. 9.87 m s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um carro de 2000k g se movendo com uma rapidez inicial de 25m / s ao longo de uma estrada horizontal desliza até parar em 60m . (a) Encontre a energia dissipada por atrito. (b) Encontre o coeficiente
Um pequeno objeto de massa m se move em um círculo horizontal de raio r sobre uma mesa rugosa. Ele está preso a uma corda horizontal fixa no centro de um círculo. A rapidez do objeto é inicialmente v
Na figura abaixo, o coeficiente de atrito cinético entre o bloco de 4,0k g e a prateleira é 0,35 . (a) Encontre a energia dissipada por atrito quando o bloco de 2,0k g cai por uma distância y . (b) En
O bloco de 2,0k g na figura desce por uma rampa curvada sem atrito, partindo do repouso a uma altura de 3,0m . O bloco então desliza por 9,0m sobre uma superfície horizontal rugosa até atingir o repou
Um bloco de massa m repousa em um plano inclinado a um ângulo θ com a horizontal (veja a figura). Uma mola com constante de força k está presa ao bloco. O coeficiente de atrito estático entre o bloco