Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 24.10 - Ex. 34
O potencial elétrico V no espaço entre duas placas paralelas. 1 e 2, é dado (em volts) por , onde x (em metros) é a distância perpendicular em relação à placa 1. Para x = 1,3 cm, (a) determine o módulo do campo elétrico; (b) o campo elétrico aponta para a placa 1 ou na direção oposta?
Passo 1
Letra (a)
Dá uma olhada no desenho:
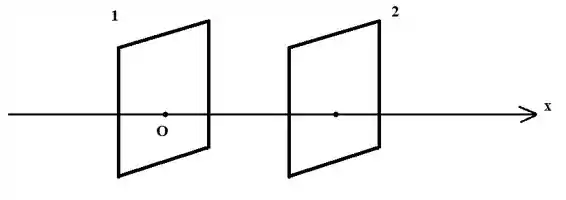
Essa é a situação, beleza? Lembra que tem uma fórmula que relaciona o campo elétrico com o potencia? Tem mais de uma, na verdade, mas a gente quer essa aqui, oh:
Antes de tudo, quero que você preste bastante atenção no sinal de menos. Ele é muito importante, e vamos precisar dele no item (b). Lembra dessa frase: “O campo elétrico é a derivada do potencial elétrico.”? Então, tá errada: é menos o potencial. Não esqueça.
Obs: Na verdade, galera, é menos o gradiente, só que quando a gente está em só uma direção, o gradiente vira uma derivada normal. Fim obs.
O lance agora é que na nossa questão, o r é x, ou seja, , porque só estamos trabalhando no eixo x, aí a fórmula fica assim:
Passo 2
Joga a expressão de V que a questão deu:
Agora substitui
Aí o módulo do campo é 39 V/m
Passo 3
Letra (b)
Lembra que eu falei do sinal de menos? Então. Pelo resultado da (a) a gente tira a conclusão que ele aponta no sentido oposto do eixo x. Olha lá na figura. Ele aponta para para a placa 1, correto? O sinal realmente importa, e não podemos esquecer. Se esquecêssemos iríamos chegar na resposta inversa.
Resposta
Letra (a):
Letra (b): Aponta para a placa 1