Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 24.1 - Ex. 36
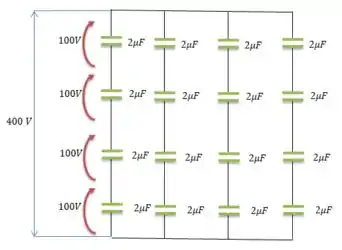
Você e seu grupo de laboratório receberam um projeto de seu professor de engenharia elétrica. Seu grupo deve projetar uma rede de capacitores que tem uma capacitância equivalente de e uma tensão de ruptura de . A restrição é que seu grupo deve usar apenas capacitores de que têm valores idênticos de tensão de ruptura de . Faça um diagrama da combinação.
Passo 1
Cara, para resolvermos esse problema, você tem que ter em mente que:
- Para associação de série de capacitores de mesma capacitância , a capacitância resultante cai para , mas as tensões máximas se somam ().
- Para associação em paralelo, a tensão continua a mesma, mas a capacitância se soma.
Então venha comigo para mais detalhes!
Passo 2
Vamos primeiro associar capacitores em série para obtermos a tensão de ruptura máxima igual ...
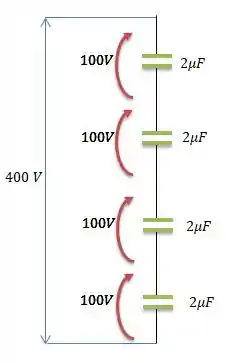
Bem, atingimos aqui a tensão de ruptura desejada, mas infelizmente a capacitância total reduziu para...
Passo 3
Para aumenta-la, mas sem alterar a tensão de ruptura, podemos adicionar ramos desse em paralelo...
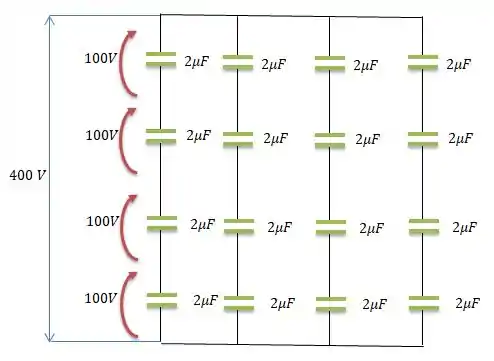
E com isso, vamos aumentar a capacitância resultante para...
Resposta
