Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 24.1 - Ex. 31
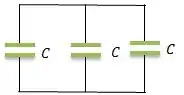
Três capacitores idênticos são conectados de forma tal que a capacitância equivalente máxima, de , é obtida.
(a) Determine como os capacitores estão conectados e faça um diagrama da combinação.
(b) Há três maneiras adicionais de conectar todos os capacitores. Faça um diagrama destas três maneiras e determine as capacitâncias equivalentes para cada arranjo.
Passo 1
Bem, uma das formas de associar esses capacitores de modo que a associação deles gera uma capacitância de é pela associação em paralelo...
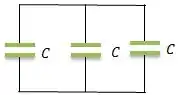
Sabemos pela teoria que em paralelo, as capacitâncias se somam...
Passo 2
Mas também podemos associar esses três capacitores de outras maneiras:
- Todos em Paralelo...
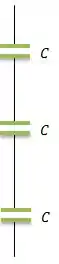
- Todos em série
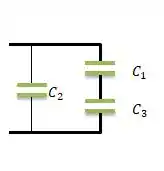
- Dois deles em série e um em paralelo com o terceiro...
Vamos ver como é cada uma dessas associações?
Passo 3
Todos em paralelo já vimos como fica...
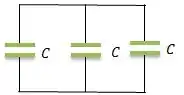
E a capacitância equivalente é
Passo 4
Todos em série seria algo do tipo...
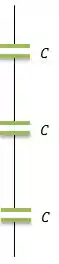
A capacitância equivalente então seria...
Passo 5
E a última forma seria associando dois em série e outro em paralelo...
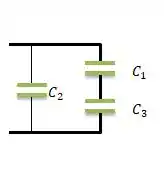
A capacitância resultante (equivalente ) seria a junção do (que é a equivalência da parte série) em paralelo com o , isto é...
OBS: O símbolo significa paralelo. Sabemos que em paralelo as capacitâncias se soma...
Passo 6
Para encontrar a , basta se lembrar de que capacitores em série possuem capacitância equivalente () através da fórmula...
Então...
Beleza, agora que já passamos por esse passo interno, podemos determinar o que queremos no exercício que é o ...
Fazendo então o paralelo entre e . Em paralelo, a resultante pode ser dada pela soma...
Então...
Como no nosso caso...
Resposta
Letra A:
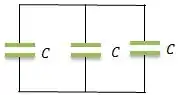
Onde
Letra B:
