Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 24.1 - Ex. 12

Dois capacitores idênticos, descarregados, estão conectados em série aos terminais de uma bateria de 100   V . Quando apenas um dos capacitores está conectado nos terminais da bateria, a energia armazenada é U 0 . Qual é energia total armazenada nos dois capacitores quando a combinação em série é conectada à bateria?

  1. 4 U 0
  2. 2 U 0
  3. U 0
  4. U 0 / 2
  5. U 0 / 4

Passo 1

Cara, vamos nesse passo 1 aqui entender o problema, pode ser?

Temos aqui um capacitor de capacitância C desconhecida conectada a uma bateria de 100   V ...

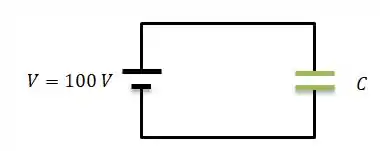
E esse capacitor, armazena uma energia U 0 que pela teoria vale...

U 0 = 1 2 C V 2   →

U 0 = 1 2 C 100 2   →

U 0 = 1 2 C 10.000   →

Ou seja...

U 0 = 5000 C

Mas aí, de repente entra outro capacitor C em série no circuito...

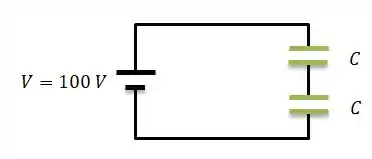
E aí a gente quer saber o que acontece com a energia U 0 do sistema. Será que ela se altera?

Passo 2

Cara... Temos dois capacitores em série. De acordo com a teoria, podemos reduzir a um circuito com apenas um capacitor C r e s resultante...

Onde a capacitância resultante vale pela teoria de série de capacitância...

1 C r e s = 1 C + 1 C   →

1 C r e s = 2 C   →

C r e s = C 2

Passo 3

Então, a energia armazenada nesse novo circuito com dois capacitores em série vale...

U = 1 2 C r e s V 2     →

U = 1 2 C r e s 100 2     →

U = 5000   C r e s

Só que C r e s = C / 2 ...

U = 5000 C 2

Porém, vimos no passo 1 que a U 0 = 5000   C , então...

U = U 0 2

Ou seja, a energia cai pela metade com a inserção de outro capacitor idêntico em série, saca?

Resposta

Letra D.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na figura abaixo, cada capacitância C 1 é igual a 6,9 μ F e cada capacitância C 2 é igual a 4,6 μ F . (a) Calcule a capacitância equivalente do circuito entre os pontos a e b. (b) Calcule a carga dos
Cada combinação de capacitores entre os pontos a e b na figura abaixo é, inicialmente, conectada a uma bateria de 120V , carregando a combinação em 120V . Essas combinações são então ligadas entre si
Dispomos de diversos capacitores de 0,25μ F . A voltagem nos terminais de cada capacitor não pode superar 600V . Você precisa montar um capacitor com capacitância de 0,25μ F , submetido a uma diferenç
Os capacitores na figura abaixo estão, inicialmente, descarregados e são conectados com indicado no diagrama com a chave S aberta. A diferença de potencial aplicada é dada por V a b = + 210V . (a) Qua
Mostre que é possível substituir o sistema de capacitores da figura por um único capacitor equivalente netre os ponstos a e b e calcule a capacitância deste capacitor.