Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 24.1 - Ex. 55
Um capacitor de é carregado a . Depois da carga, o capacitor é desconectado da fonte de tensão e é conectado aos terminais de um segundo capacitor que havia sido previamente descarregado. A tensão final no capacitor de é .
(a) Qual é a capacitância do segundo capacitor?
(b) Quanta energia foi dissipada quando a conexão foi feita?
Passo 1
Para resolver esse exercício, vamos imaginar o seguinte: o primeiro capacitor já está carregado e com diferença de potencial ...
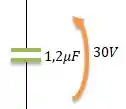
Ao se conectar ao segundo capacitor...
Perceba que a tensão que estava em cima do primeiro () se reduz para (). O que aconteceu basicamente foi de que a energia armazenada no primeiro capacitor se dividiu uma parcela para cada capacitor.
Sabendo disso e também sabendo de que os que estão em cima do capacitor também está em cima do capacitor , pelo fato de estarem ligados um ao outro formando uma malha, podemos então resolver o problema, vamos nessa?
Passo 2
POW! Eu disse ali no passo 1 que o que aconteceu foi que a energia inicial armazenada no capacitor de foi dividida para os dois capacitores após serem ligados, isto é...
E a energia final é a soma da energia nos dois capacitores.
Tendo em mente que a energia num capacitor pode ser dada por ...
Onde é a tensão em cima do capacitor inicial () e é a tensão após os capacitores se conectarem (). Quando as capacitâncias, , é a que queremos descobrir, saca?
Substituindo na equação...
Essa então que é a capacitância do segundo capacitor, ta ligado?
.
Passo 3
A energia dissipada é a energia que saiu do capacitor para ser armazenada no capacitor ...
Como a tensão no capacitor é ...
Resposta
Letra A:
Letra B: