Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 24.1 - Ex. 56

Um capacitor de 12 μ F e um capacitor de capacitância desconhecida são ambos, carregados a 2,00   k V . Depois da carga, os dois capacitores são desconectados da fonte de tensão. Os capacitores são, então, conectados um ao outra placa positiva à placa negativa e placa negativa à placa positiva. A tensão final nos terminais do capacitor de 12   µ F é 1,00   k V .

(a) Qual é a capacitância do segundo capacitor?

(b) Quanta energia foi dissipada quando a conexão foi feita?

Passo 1

Cara, o problema nos disse que inicialmente tínhamos dois capacitores carregados com a mesma tensão 2,00   k V ...

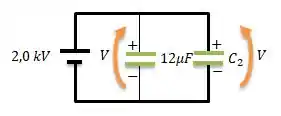
Lembrando que a tensão sempre é maior na placa positiva.

Em seguida, a gente conecta a placa positiva de uma na negativa da outra e vice versa...

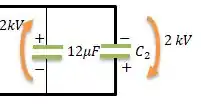
Bem... Repare então que uma placa vai tender a neutralizar a outra fazendo então surgir uma corrente no circuito. A corrente só vai parar quando as tensões se igualarem a V = 1,0 k V nos dois ramos...

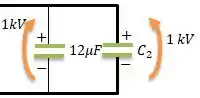
E o nosso intuito aqui é encontrar esse C 2 sabendo desse rolê todo , ta ok?

Passo 2

POW! Sabemos que a tensão se relaciona com capacitância por Q = C V , então se as tensões no final do processo atingem V = 1,0   k V , então podemos falar que para os dois capacitores é válida a relação...

1,0   k V = Q 1 C 1 = Q 2 C 2   →

Então a capacitância C 2 que queremos encontrar será...

C 2 = Q 2 1,0   k V

Agora... Quem são as cargas Q 1 e Q 2 ?

Essas são as cargas que se encontram na placa depois de muito tempo que os capacitores se encontram conectadas.

Se você reparar no sistema assim que conectamos os dois capacitores...

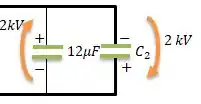
A carga negativa antes tende a neutralizar a carga positiva do outro capacitor, e o que sobra de carga no circuito após partes das cargas se neutralizarem é Q 1 + Q 2 , saca?

Q 1 + Q 2 = Q 2 i n i c i a l - Q 1 i n i c i a l

Q 2 i n i c i a l - Q 1 i n i c i a l significa justamente isso, que partes das cargas positivas vai cancelar com as cargas negativa do outro lado. Então bora calcular esses valores iniciais de cargas aí...

Passo 3

Pela teoria de capacitores, sabemos que...

Q 2 i n i c i a l = C 2 V i n i c i a l   →

Inicialmente no capacitor C 2 a tensão é V i n i c i a l = 2 k V = 2 ⋅ 10 3   k V ...

Q 2 i n i c i a l = C 2 ⋅ 2 ⋅ 10 3     →

Q 2 i n i c i a l = 2 C 2 ⋅ 10 3

E na placa 1 , a quantidade de cargas nela será...

Q 1 i n i c i a l = C 1 V i n i c i a l   →

Q 1 i n i c i a l = 12 ⋅ 10 - 6 ⋅ 2 ⋅ 10 3     →

Q 1 i n i c i a l = 24 ⋅ 10 - 3 = 24   m C

Então veja bem, quando as placas são conectadas inversamente, após um tempo ligadas, a carga que vão sobrar sem se neutralizar será...

Q 1 + Q 2 = 24 ⋅ 10 - 3 - 2 C 2 ⋅ 10 3

Passo 4

Então voltando para a equação que determinamos no passo 2...

V = Q 1 C 1 = Q 2 C 2   →

Q 1 = C 1 Q 2 C 2   →

Substituindo nessa equação do passo 3...

C 1 Q 2 C 2 + Q 2 = 24 ⋅ 10 - 3 - 2 C 2 ⋅ 10 3

Como C 1 = 12   μ F ...

12 ⋅ 10 - 6 Q 2 C 2 + Q 2 = 24 ⋅ 10 - 3 - 2 C 2 ⋅ 10 3   →

Só que sabemos do passo 2 que...

C 2 = Q 2 1,0   k V     o u       Q 2 C 2 = 1 ⋅ 10 3

Então...

12 ⋅ 10 - 6 1 ⋅ 10 3 + 1 ⋅ 10 3 C 2 = 24 ⋅ 10 - 3 - 2 C 2 ⋅ 10 3   →

Resolvendo essa equação...

12 ⋅ 10 - 3 + C 2 ⋅ 10 3 = 24 ⋅ 10 - 3 - 2 C 2 ⋅ 10 3   →

C 2 ⋅ 10 3 + 2 C 2 ⋅ 10 3 = 24 ⋅ 10 - 3 - 12 ⋅ 10 - 3 →

3 C 2 ⋅ 10 3 = 12 ⋅ 10 - 3 →

C 2 = 12 3 ⋅ 10 - 3 10 3 →

C 2 = 4 ⋅ 10 - 6   →

Ou ainda...

C 2 = 4   μ F

Passo 5

L e t r a   B :

A energia que vai ser dissipada U d i s s i p a d a vai ser a energia que está armazenada em cada capacitor antes U A n t e s   das conexões serem feitas menos a energia depois que o sistema se equilibrar U D e p o i s .

Vamos primeiro calcular a energia armazenada em cada capacitor antes então...

U A n t e s = U 1 + U 2   →

U A n t e s = 1 2 C 1 V 2 + 1 2 C 2 V 2 →

U A n t e s = 1 2 V 2 C 1 + C 2 →

U A n t e s = 1 2 2,00 ⋅ 10 3 2 12 ⋅ 10 - 6 + 4 ⋅ 10 - 6 →

Calculando isso aí...

U A n t e s = 1 2 4 ⋅ 10 6 16 ⋅ 10 - 6 →

U A n t e s = 2 ⋅ 16 →

U A n t e s = 32   J

Agora, considerando que a nova tensão vale 1   k V vamos recalcular as energias...

U D e p o i s = U 1 + U 2   →

U D e p o i s = 1 2 C 1 V 2 + 1 2 C 2 V 2 →

U D e p o i s = 1 2 V 2 C 1 + C 2 →

U D e p o i s = 1 2 1 ⋅ 10 3 2 12 ⋅ 10 - 6 + 4 ⋅ 10 - 6 →

Calculando isso aí...

U D e p o i s = 1 2 1 ⋅ 10 6 16 ⋅ 10 - 6 →

U D e p o i s = 1 2 ⋅ 16 →

U D e p o i s = 8   J

Então a energia dissipada será...

U d i s s i p a d a = 32   J - 8   J = 24   J

Resposta

Letra A:

C 2 = 4   μ F

Letra B:

U d i s s i p a d a = 24   J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os capacitares da Fig. Abaixo estão inicialmente descarregados. As capacitâncias são C 1=4,0μ F , C 2=8,0μ F e C 3=12μ F e a diferença do potencial da bateria é V =12V . Quando a chave S é fechada, qu
A figura mostra um capacitar variável com “dielétrico de ar” do tipo usado para sintonizar manualmente receptores de rádio. O capacitar é formado por dois conjuntos de placas intercaladas, um grupo de
Na figura, uma diferença de potencial V = 100,0 V é aplicada ao circuito e os valores das capacitâncias são C 1 = 10,0 μF, C 2 = 5,00 μF e C 3 = 4,00 μF. Se o capacitor 3 sofre uma ruptura dielétrica
A Fig. abaixo mostra uma bateria de 12,0V e três capacitares descarregados de capacitâncias C 1=4,00μ F , C 2=6,00μ F e C 3=3,00μ F . A chave é deslocada para a esquerda até que o capacitar 1 esteja t
O capacitar 3 da Fig. (a) é um capacitar variável (é possível fazer variar a capacitância C 3 ). A Fig. (b) mostra o potencial elétrico V 1 entre as placas do capacitar 1 em função de C 3 . A escala h