Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 21.Problemas - Ex. 104c
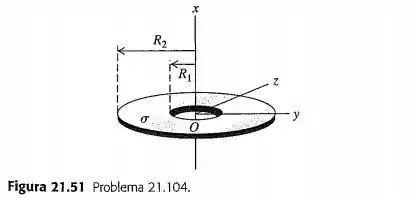
Denomina-se coroa anular um disco fino de raio externo com um buraco circular concêntrico de raio interno (Figura ). Uma coroa anular possui uma densidade superficial de carga sobre sua superfície. Determine a carga total sobre a coroa anular. A coroa anular está sobre o plano com seu centro na origem. Para um ponto arbitrário sobre o eixo (o eixo de simetria da coroa anular), determine o módulo, a direção e o sentido do campo elétrico . Considere todos os pontos acima e abaixo do plano da coroa anular da Figura . Mostre que, para os pontos sobre o eixo suficientemente próximos da origem, o módulo do campo elétrico é aproximadamente proporcional à distância entre o centro da coroa e o ponto considerado. Qual é a distância que pode ser considerada “suficientemente próxima”? Uma partícula puntiforme com massa e carga pode se mover livremente sobre o eixo (mas não pode sair desse eixo). A partícula é inicialmente colocada sobre o ponto e, a seguir, liberada. Determine a frequência das oscilações da partícula. (Sugestão: faça uma revisão da seção . A coroa anular permanece em repouso.)
Passo 1
Como foi obtido, o campo elétrico neste exercício é dado por:
Para resolver este caso, consideramos o campo de um disco uniformemente carregado:
E analisando o termo
Pode-se manipular a forma como ele é escrito. Primeiro iguala-se o denominador do termo dentro da raiz quadrada:
Agora, dividindo ambos o numerador quanto o denominador por :
Tal que, para os pontos muito próximos da origem, , então:
Passo 2
Dito isso, o campo resultante pode ser reescrito substituindo os termos dependentes dos raios:
Que, tirando o termo em comum:
O que torna o módulo do campo elétrico proporcional à distância do centro da coroa até um certo ponto.
Passo 3
Com a ideia de um ponto suficientemente próximo da origem, temos:
Ou seja, a distância “suficientemente próxima” é: