Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 6.1 - Ex. 1
Você empurra um livro de física por sobre uma mesa horizontal com um impulso horizontal de , enquanto a força de atrito em oposição é de . Qual é o trabalho realizado por cada uma das seguintes forças sobre o livro: (a) seu impulso de , (b) a força de atrito, (c) a força normal da mesa e (d) a gravidade? (e) Qual é o trabalho resultante realizado sobre o livro?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente determinar o trabalho de algumas forças. Para isso, você precisa lembrar que o trabalho de uma força constante é dado por:
Onde é a força aplicada e é o deslocamento realizado.
A seguir vamos desenhar todas as forças que agem sobre o livro:
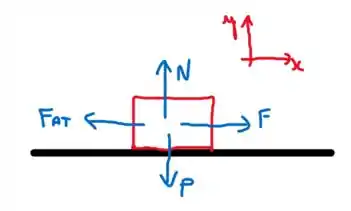
Escrevendo vetorialmente, temos que
Onde é a força aplicada por você no livro, é a força de atrito entre a superfície e o livro, é a força normal de contato e o peso do livro. Além disso, temos representando os vetores na direção horizontal e na vertical.
Já o deslocamento é dado por:
Com isso, vamos calcular o trabalho de cada força fazendo o produto escalar entre as forças e o deslocamento. Depois, basta substituir os valores dados pelo enunciado.
Vamos lá!
Passo 2
Fazendo o produto entre as forças vistas no passo e o vetor deslocamento, vamos ter as equações:
Onde é o trabalho realizado pela força .
Que é o trabalho realizado pela força de atrito.
Trabalho realizado pela força , que é nulo porque não realiza deslocamento.
E o trabalho realizado pela força peso, que é nulo pelo mesmo motivo da força .
Passo 3
Como e , segue que
Já para o atrito, temos , de modo que
Por fim, o trabalho total é a soma dos trabalhos:
Portanto,
Valeu, galera! Até a próxima! 😉