Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 22.Problemas Adicionais - Ex. 66
Três partículas com a mesma carga positiva formam um triângulo equilátero de lado . Qual é o módulo do campo elétrico produzido pelas partículas no ponto médio de um dos lados?
Passo 1
E aí, galerinha! 😁
Nesse problema temos três partículas com a mesma carga positiva formam um triângulo equilátero de lado e nosso objetivo é obter o módulo do campo elétrico produzido pelas partículas no ponto médio de um dos lados.
Parece complicado? 🤔
Para visualizar melhor o problema do enunciado, vamos representá-lo em uma figura:
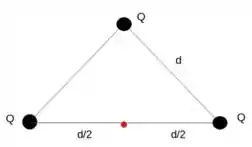
Para calcular o campo elétrico no ponto médio, basta utilizar o princípio da superposição, ou seja, calcular o campo exercido por cada uma das cargas e somar todos eles no ponto que a gente tá analisando.
Veja só! 😁
Passo 2
Como todas as cargas são positivas, as linhas de campo elétrico delas sempre apontam para fora.
Olha pra essas duas cargas na mesma linha que o ponto que desejamos calcular o campo, as duas geram esses campos:
O campo elétrico é dado pela equação:
Onde:
é a carga elétrica;
é a distância entre o ponto que desejamos calcular o campo e a carga que gera esse campo e
é uma constante elétrica chamada permissividade elétrica no vácuo.
Bora lá! 😉
Passo 3
Como as distâncias entre o ponto e as cargas são iguais, e as cargas são iguais temos o mesmo campo elétrico naquele ponto gerado pelas cargas 1 e 2 já que o campo só depende da carga e da distância.
E como vimos na figura, esses vetores campo elétrico possuem sentidos opostos, logo vão se anular:
Assim, os campos gerados pelas cargas mais próximas se cancelam sobrando apenas a carga mais distante, dessa forma:
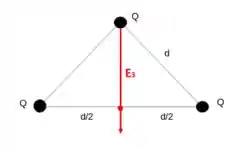
E podemos calcular o módulo desse campo usando a equação:
A distância entre a carga e o ponto onde desejamos calcular podemos tirar fazendo o teorema de Pitágoras.
Não precisa extrair a raiz aqui, lembra que usamos na fórmula?
Logo, podemos substituir o valor de na expressão do campo elétrico:
Assim, chegamos finalmente na expressão do campo elétrico:
Essa questão pediu apenas o módulo do campo elétrico, mas se você quiser, ainda pode responder que o sentido desse campo elétrico é para baixo! ;)
E aí! o que achou? Responde Aí! 😊
