Três partículas são mantidas fixas em um eixo . A partícula , de carga , está em ; a partícula , de carga , está em . Determine a razão para que a força eletrostática a que está submetida a partícula seja nula (a) se a partícula estiver no ponto ; (b) se partícula estiver no ponto
Passo 1
Nesse caso, a gente tem a seguinte situação:
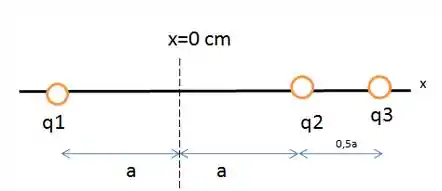
Para que a força horizontal sobre seja nula a equação de equilíbrio das forças deve ser respeitada:
A partir daqui calcularemos a força elétrica usando:
Passo 2
Vamos calcular agora as forças usando a equação da força elétrica para cada combinação e depois faremos o somatório das forças.
Somando as forças temos:
Então, dividindo essa equação por , a gente encontra o seguinte:
Daí:
Resposta
(b)