Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 3.3 - Ex. 43

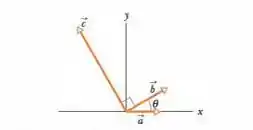
Os três vetores na Fig. 3-33 têm módulos a   =   3,00   m , b   =   4,00   m e   c   =   10,0   m ; θ = 30,0 ° . Determine (a) a componente x e (b) a componente y de a → ; (c) a componente x e (d) a componente y de b →   ; (e) a componente x e (f) a componente y   de c → . Se c → = p a →   + q b → , quais são os valores de (g) p e (h) q ?

Passo 1

Podemos ver na figura que c →   é perpendicular a b → , o que significa que o ângulo entre c → e o semieixo x positivo é θ = 90 ° . Na notação dos vetores unitários, os três vetores são

a → = a x i →

b → = b x i → + b y j → = b cos ⁡ θ i → +   b sen ⁡ θ j →

c → = c x i → +   c y j → = c cos ⁡ θ + 90 ° i → +   c sen ⁡ θ + 90 ° j →

Passo 2

Dessa forma ,

A componente x de a →   pode ser entendida como a x = a cos ⁡ 0 ° = a = 3,00   m

Passo 3

A componente y de a →   , por sua vez , é representada por a y = a sen ⁡ o ° = o

Passo 4

A componente x de b →   , da mesma forma que no primeiro item, pode ser calculada através da relação b x = b cos ⁡ 30 ° = 4,00   m cos ⁡ 30 ° = 3,46   m

Passo 5

A componente y de b →     por outro lado , é b y = b sen ⁡ 30 ° = 4,00   m   sen ⁡ 30 ° = 2,00   m

Passo 6

A componente x de c →   é c x = c cos ⁡ 120 ° = 10 m   cos ⁡ 120 ° = - 5,00   m

Passo 7

A componente y de c →   é c y = c sen ⁡ 120 ° = 10 m   sen ⁡ 120 ° = 8,66   m

Passo 8

Substituindo os valores das componentes , temos que :

- 5,0   m = p 3,0   m +   q ( 3,46   m )

8,66   m = q   ( 2,0   m )

Resolvendo esse sistema , obtemos :

p =   - 6,67  

q = 4,33

De boa , galera ??? Bora fazer mais exercícios então

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um trem com uma velocidade constante de 60,0k m / h se move na direção leste por 40,0m i n , depois em uma direção que faz um ângulo de 50,0 º º a leste com a direção norte por 20,0m i n e, finalmente
Determine a soma dos quatro vetores a seguir (a) em termos dos vetores unitários e em termos (b) do módulo e (c) do ângulo. A=( 2,00m ) i ^+( 3,00m ) j ^C=( - 4,00m ) i ^+( - 6,00m ) j ^ B:4,00me+ 65,
O vetor A → está a 34,0 ° em sentido anti-horário do eixo - y . O componente x de A → é A x = - 16,0 m.Qual é o componente y de?Qual é o módulo de A → ?
O vetor A → tem componente y A y = + 9,60 . A → forma um ângulo de 32,0 ° em sentido anti-horário a partir do eixo + y .Qual é o componente x de A → ?Qual é o módulo de A → ?
Determine o módulo, a direção e o sentido dos vetores representados pelos seguintes pares de componentes: (a) Ax = 8,60 cm, Ay = 5,20 cm; (b) Ax = 9,70 m, Ay = 2,45 m; (c) Ax = 7,75 km, Ay 2,70 km.