Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 51
50. Uma roda de de diâmetro rola a . Qual é o valor da velocidade do ponto frontal da borda da roda?
Passo 1
Imagine uma roda girando no asfalto...
Em todos os pontos dessa roda, temos ao mesmo tempo rotação e translação. Para o ponto frontal dessa roda, os vetores de direção das velocidades estão aqui desenhados pra você:
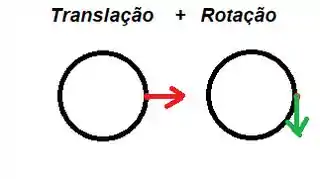
Essas velocidades se combinam formando uma velocidade resultante representado em azul nessa outra figura aqui:
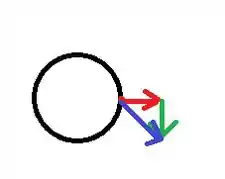
Então a velocidade em azul, será a velocidade resultante que buscamos, pois é a velocidade final do ponto frontal!
A velocidade em vermelho é a velocidade do ponto de centro de massa:
Enquanto que a velocidade em verde é a velocidade de rotação:
Vale a pena lembrar, vale a pena lembrar que em um movimento combinado, , como vimos no capítulo!
Passo 2
A velocidade em azul pode ser dada então pela soma vetorial das outras duas...
Então...
Se a bola rola a , então...
E...