Uma partícula em uma caixa unidimensional com comprimento L está no primeiro estado excitado (n = 2). (A caixa tem uma extremidade na origem e a outra extremidade no eixo x positivo.) (A) Esboço ψ 2 (x) versus x para esse estado. (b) Qual é o valor esperado
Passo 1
(a) Então, vamos plotar , onde:
Assim:
O gráfico é:
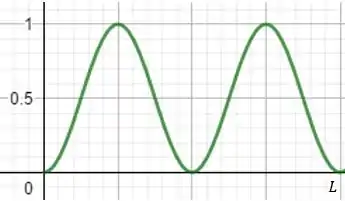
Passo 2
(b) Para resolver essa questão, vamos usar:
Onde, no primeiro estado excitado:
Assim, para e uma caixa com comprimento :
Calma, essa integral é tabelada, o máximo que precisa fazer é a substituição :
e
E o resultado dessa integral é:
Passo 3
(c) A probabilidade é dada pela:
Então, queremos a probabilidade para :
Passo 4
(d) A diferença entre as duas letras anteriores é que em (b) temos um valor médio da medições das posições da partícula, mesmo que a probabilidade da partícula estar nessa posição seja .
Então, as respostas da (b) e da (c) não são contraditórias.
Resposta
(a) 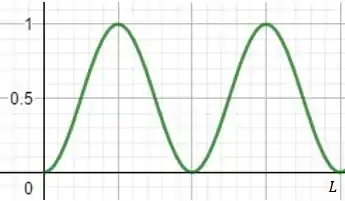
(b)
(c)
(d) Não são contraditórias.