Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 131
VÁRIOS PASSOS. Você está em um parque de diversões com suas costas apoiadas contra a parede de um cilindro vertical girante. O chão se abre e você é mantido pelo atrito estático. Sua massa é de . (a) Desenhe um diagrama de corpo livre para você próprio. (b) Use este diagrama, junto com as leis de Newton, para determinar a força de atrito sobre você. (c) Se o raio do cilindro é e o coeficiente de atrito estático entre você e a parede é , qual é o menor número de voltas por minuto necessário para evitar que você deslize parede abaixo? Esta resposta só vale para você? Outras pessoas, mais massivas, cairão? Explique.
Passo 1
A aplicação da segunda lei de Newton e a definição da força máxima de atrito estático será usada para determinar o período do movimento. O inverso do período nos dará o número mínimo de revoluções necessárias por unidade de tempo para mantê-lo no lugar.
Passo 2
Item (a)
O diagrama de corpo livre mostrando abaixo nos indica as forças agindo em você quando você está sendo mantido no lugar pela força máxima de atrito estático.
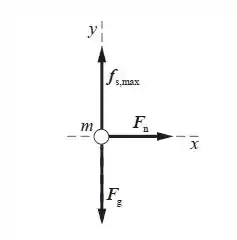
Passo 3
Item (b)
Aplicando para si mesmo enquanto você está preso por atrito, no eixo x:
E no eixo y:
Substituindo os valores numéricos nessa equação acima, para achar a força de atrito máxima:
Passo 4
Item (c)
O número de revoluções por minuto é o inverso do período em minutos:
Pela definição de força de atrito estática , pela equação das somas das forças em x:
Como velocidade é , e você estará fazendo movimentos circulares, então:
Substituindo na equação ali de cima:
Substituindo na expressão de :
Agora, substituindo por valores numéricos:
Como a sua massa não aparece na expressão para , esse resultado vale para todas as pessoas, independentemente da sua massa.