Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 1.Problemas - Ex. 21
Verifique o resultado da experiência do Puy de Dome, realizada por Périer em 1648.
Passo 1
Essa questão está discutindo um experimento que foi mencionado no livro.
No experimento, Périer levou um barômetro de mercúrio para o topo de uma montanha com de altura. E observou que a altura inicial de da coluna diminuía em .
Nosso objetivo aqui é verificar que esse resultado faz sentido. Vamos começar lembrando da “fórmula” que dá a pressão atmosférica a partir de um barômetro de mercúrio:
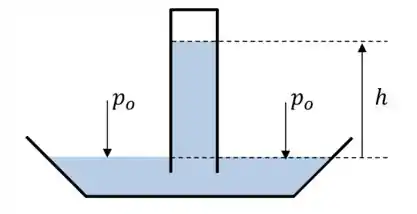
Temos que simplesmente igualar a pressão atmosférica à pressão gerada pela coluna de mercúrio:
Passo 2
Antes de subir a montanha, a pressão atmosférica seria dada pela seguinte fórmula:
Onde é a altura da coluna de mercúrio naquele momento.
Depois de subir a montanha, a altura da coluna é reduzida em , então a nova pressão atmosférica é:
Então a razão entre a pressão antiga e a nova deveria ser:
Passo 3
Agora vamos verificar se esse resultado está de acordo com a realidade. Precisamos consultar alguma tabela (ou calculadora online) que dê a pressão atmosférica em função da altitude.
Pesquisando um pouco, achamos que a pressão atmosférica na altitude e é:
Supondo que a temperatura continua mais ou menos constante, encontramos que a pressão na altitude e é:
Então a razão “verdadeira” entre as pressões é:
Que é bastante próximo do resultado sugerido pelo experimento de Périer.
Essa pequena diferença provavelmente se deve às nossas aproximações: de que a temperatura não muda com a altitude, de que a montanha tem exatamente de altura, etc.
Resposta
O experimento sugere que a razão entre as pressões no solo e no topo da montanha é aproximadamente . O valor conhecido atualmente dá uma razão próxima de .