Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 1.1 - Ex. 52
Um vetor 7,0 unidades de comprimento e um vetor com 5,5 unidades dde comprimento são somados. Sua soma é um vetor com 10,0 unidades de comprimento. (a) Mostre graficamente pelo menos uma maneira pela qual esses vetores podem ser somados. (b) Usando seu esboço da Parte (a), determine o âgulo entre os dois vetores originais.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O que ele quer é que a gente faça um esboço de uma soma vetorial que tenha as características do enunciado.
Vamos chamar de o vetor de 7 unidades e o vetor com 5,5 unidades. O vetor será o vetor resultante da soma e portanto vale 10 unidades.
O esboço dessa soma pode ser um triângulo, que é dado por:
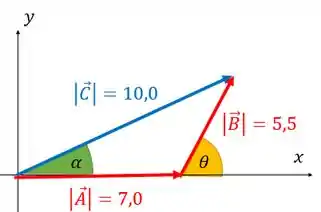
Repara que o começa no final do vetor . E o vetor começa no inicio do vetor e termina no final do vetor .
A gente colocou o vetor paralelo ao eixo só para facilitar as continhas futuras, tá?
Prontinho, é assim que podemos representar nossa soma vetorial.
Passo 2
b) Para descobrir o ângulo entre e , temos que lembrar que se
Então vale que
Podemos achar essas componentes dos vetores usando os ângulos que estão na nossa figura.
- Para o vetor .
Como ele está paralelo ao eixo , a componente dele é o próprio módulo do vetor. E a componente em vai ser zero.
- Para o vetor .
O ângulo que dá a orientação desse vetor é o . Como o ângulo está colado no eixo , a componente vai ser o valor do módulo do vetor vezes o cosseno de :
E a componente vai usar o seno
- Para o vetor .
O ângulo que dá a orientação desse vetor é o . Ele está colado em , então vamos usar o cosseno para e o seno para :
Passo 3
Voltando as nossas equações
Substituindo as componentes, temos:
Elevando ao quadrado e somando as equações, temos:
Usando, , temos: