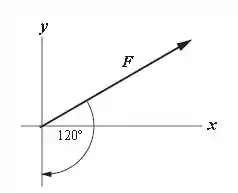
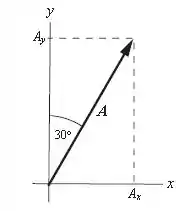
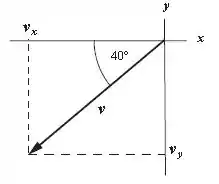
Determine as componentes e dos seguintes três vetores do plano . (a) Um vetor deslocamento de que forma um ângulo de no sentido horário a partir do eixo . (b) Um vetor velocidade de que forma um ângulo de no sentido anti-horário com eixo . (c) Uma força de 40 lb que forma um ângulo de no sentido anti-horário com o eixo .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
As componentes x e y desses vetores, são exatamente suas projeções nestes eixos, e são encontradas a partir do ângulo. Para o item (a) temos:
Passo 2
Para o item (b) temos:
Passo 3
Para o item (c) temos: