Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.8 - Ex. 43a
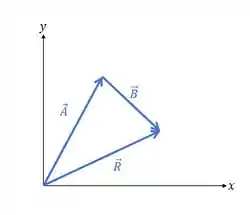
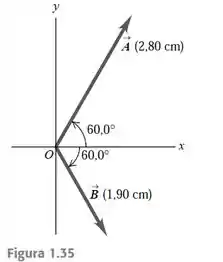
O vetor possui comprimento igual a e está no primeiro quadrante a acima do eixo . O vetor possui comprimento igual a e está no quarto quadrante a
abaixo do eixo (Figura 1.35). Use componentes para encontrar o módulo e a direção de a) ; b) ; c) . Em cada caso faça um diagrama da soma ou da diferença e mostre que os resultados concordam aproximadamente com as respostas numéricas obtidas.
Passo 1
E aí, galerinha!
Nesse problema temos dois vetores e nosso objetivo é calcular a soma entre eles e obter o modulo e direção do vetor resultante.
Tem ideia de como fazemos isso? 😬
Vamos fazer uma analise e escrever os vetores em termos de suas componentes e .
O vetor faz ângulo de com , no primeiro quadrante;
O vetor faz ângulo de com , no quarto quadrante.
Vamos usar o sinal (para indicar a direção do componente vetores:
Veja só! 🤔
Passo 2
- Para encontrarmos a componente resultante, , em e basta somar as correspondentes componentes.
Então temos que:
Como já conhecemos as componentes resultante, , em e , vamos calcular o módulo para encontrar a resultante do vetor .
Bacana, não é?
Passo 3
Vamos calcular a direção do vetor :
Sabemos que para isso, vamos utilizar a relação:
E sabemos que:
Então:
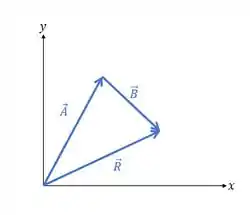
Decompondo as componentes, o diagrama fica da seguinte forma:
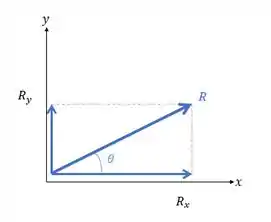
A resultante, , está no primeiro quadrante, com , confirmando nosso calculo.
E aí! o que achou? Responde Aí! 😐
Resposta
