Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 3.Exercícios e Problemas - Ex. 5

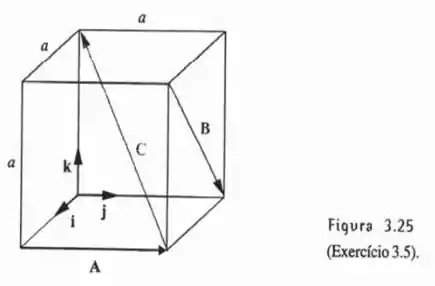
A) Escreva a expressão analítica dos vetores A,B e C da figura 3.25.

B) Determine os ângulos θ entre A e B e ∅ entre B e C.

Passo 1

Resolução da letra A).

Meus caros, para responder a letra A não há muita dificuldade pelo fato de que os vetores tem módulos iguais as arestas do cubo!

A = a j

B = a ( - i - k )

C = a ( - i - j + k )

Passo 2

Resolução da letra B).

Pelo produto escalar:

B ∙ C = b x c x + b y c y + b z c z = a 2 - a 2 = 0

B ∙ C = B ∙ C ∙ cos ⁡ ∅

Onde:

B = b x 2 + b y 2 + b z 2

Logo:

B ∙ C = a 2 ∙ a 3 ∙ c o s ⁡ ( ∅ )

0 = a 2 6 c o s ⁡ ( ∅ )

cos ⁡ ∅ = 0

Portanto ∅ = 90 ° .

A ∙ B = A ∙ B ∙ c o s ⁡ ( θ )

- a 2 = a 2 2 ∙ c o s ⁡ ( θ )

cos ⁡ θ = - 2 2

Logo θ = 135 °

Resposta

A)

A = a j

B = a ( - i - k )

C = a ( - i - j + k )

B)

∅ = 90 °   e     θ = 135 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As dimensões de uma sala são 3,00m (altura) X 3,70m X 4,30m . Uma mosca parte de um canto da sala e pousa em um canto diagonalmente oposto. (a) Qual é o módulo do deslocamento da mosca? (b) A distânci
A componente x do vetor A → é - 25,0m e a componente y é + 40,0m . (a) Qual é o módulo de A → ?(b) Qual é o ângulo entre a orientação de A → e o semieixo x positivo?
Um carro viaja 50k m para leste, 30k m para o norte e 25k m em uma direção 30 ° a leste do norte. Desenhe o diagrama vetorial e determine (a) o módulo e (b) o ângulo do deslocamento do carro em relaçã
(a)Determine a soma a → + b → , em termos de vetores unitários, para a → = 4,0m i ^ + ( 3,0m ) j ^ e b ^ = 13,0m i ^ + ( 7,0m ) j ^ . Determine (b) o módulo e (c) a orientação de a → + b → .
Três vetores, a → , b → e c → , têm o mesmo módulo, 50m , e estão em um plano x y . Os ângulos dos vetores em relação ao semieixo x positivo são 30 ° , 195 ° , e 315 ° , respectivamente. Determine (c)