Ao seguir um mapa do tesouro, você parte de um velho carvalho. Primeiro, caminha diretamente para o sul, depois vira e segue a do oeste para o norte e, finalmente, caminha a do norte para o leste, onde encontra o tesouro: uma biografia de Isaac Newton!

a) Para retornar ao velho carvalho, em que direção deve ir e qual distância deve percorrer? Use os componentes para resolver este problema.

b) Para conferir o seu cálculo na parte (a), desenhe uma solução gráfica aproximada em escala.

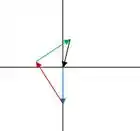
b) Repara que você anda em três direções diferentes seguindo o enunciado. Primeiro a gente vai para o sul (vetor azul - ), depois para oeste (vetor vermelho - ) e por fim para leste (vetor verde -)

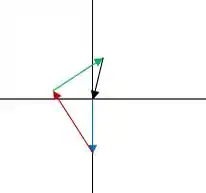
Esse vetor preto é o nosso vetor de deslocamento para voltar à origem ( ).

Agora que entendemos a figura, vamos para letra a.

Tranquilo até aqui?

1. O problema nos descreve três trajetórias. A ideia aqui é colocar essas trajetórias dadas em um sistema de coordenadas e descobrir qual vetor melhor descreve cada uma. Vou chamá-las de vetores e .

A soma desses vetores será outro vetor (), que é o nosso deslocamento total. Logo:

Esse vetor , é um vetor único que substitui todos os deslocamentos anteriores, como se estivéssemos indo diretamente do ponto inicial ao ponto final dessa trajetória.

Sendo assim, podemos pensar que para voltar à origem, após se deslocar , devemos nos deslocar no sentido contrário, certo? Logo, o que queremos é .

E para descobrirmos a distância percorrida para voltar, precisamos apenas calcular o tamanho desse vetor , ent��o queremos o módulo desse vetor:

Bacana, não é?

(a) As trajetórias listadas no enunciado são:

-Caminhar diretamente para o sul por , ou seja, se associarmos o sul a parte negativa do eixo , o vetor é

- Seguir a do Oeste para o norte, ou seja, temos a partir do eixo positivo em direção ao eixo negativo. Com isso, o vetor vai ter as duas componentes. A componente vertical está relacionada com o cosseno de , no sentido positivo do eixo , e a componente horizontal com o seno de , pro lado negativo do eixo horizontal.

- por fim, você caminha a do norte para o leste, ou seja, a partir da parte positiva do eixo , temos . Logo, o vetor terá também duas componentes. Ambas positivas: a componente horizontal relacionada com o cosseno de e a vertical com o seno de .

Bora para soma!

Agora vou adicionar a esses:

Em termos das componentes temos:

Substituindo os valores das componentes temos o seguinte:

Ficamos com duas expressões: uma para cada componente do vetor que a gente ainda não conhece. Agora é só isolar a componente de em cada expressão e jogar tudo na calculadora:

Esse é o vetor que representa o que andamos até chegar no tesouro. Então, para voltar para a origem, precisamos fazer o caminho inverso, logo o :

E o módulo do vetor é:

Estamos quase lá!

Então, precisamos andar mais metros! Mas em qual direção? Isso a gente acha pelo ângulo!

Olha só o desenho desse vetor:

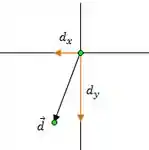
O ângulo em relação ao eixo na parte é e podemos achar a tangente desse ângulo, fazendo a razão entre as componentes horizontal e vertical, saca só:

Então, devemos andar mais metros na direção de oeste para o sul.

E aí! O que achou? Responde Aí! 😉