Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 3.Problemas Adicionais - Ex. 53
Os vetores e estão no plano , tem módulo e ângulo . tem componentes e . Determine o snauglo entre o semi eixo negativo e (a) o vetor . (b) o vetor e (c) o vetor .
Passo 1
Belezera galerinha, como o enunciado nos deu o módulo do vetor e o ângulo que ele faz com o semi-eixo positivo , podemos encontrar suas componentes, tais que:
E no eixo :
Logo, podemos escrever o vetor em termos dos vetores unitários:
Portanto, os dois vetores e que iremos trabalhar, são:
Passo 2
Como o enunciado nos deu que o vetor faz um ângulo de com o semi-eixo positivo :
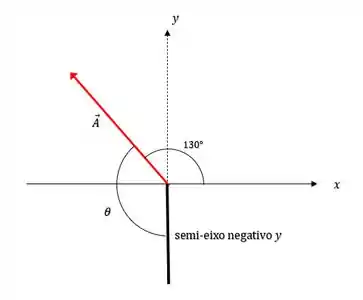
O ângulo que o vetor faz com o semi eixo negativo é dado de acordo com a figura por , logo:
Iradoso, agora para o temos que o ângulo que ele faz com o semi-eixo negativo é dado como:
Tal que:
Passo 3
Agora na letra (b), teremos que o produto vetorial entre e será:
Ou seja, o vetor resuntante do produto vetorial, possui componente somente em , no eixo , fora do plano . Isso quer dizer que esse vetor resultante é perpendicular aos vetores e , de modo que o ângulo que esse vetor faz com o semi eixo negativo é .
Passo 4
Belezoca, agora no item (c), queremos o ângulo que o vetor faz com o semi-eixo negativo , então primeiro vamos calcular esse produto vetorial, tal que:
E agora pra gente calcular o ângulo que esse vetor faz com o semi-eixo negativo , vamos precisa lembrar da relação do ângulo entre dois vetores e , dada como:
O vetor é o vetor que encontramos:
Enquanto que o vetor será o semi-eixo negativo :
Logo:
Portanto, o ângulo que o vetor faz com o semi-eixo negativo será dado como: