O vetor tem um módulo de 12,0m e faz um ângulo de 60,0° no sentido anti-horario com o semi eixo positivo x de um sistema de coordenadas xy. O vetor é dado por no mesmo sistema de coordenadas. O sistema de coordenadas sofre uma rotação de 20,0° no senido ani-horario em torno da origem para formar um sistema . Detrmine os vetores (a) e (b) em termos dos vetores unitários do novo sistema.
Passo 1
Então pessoal , vamos dar uma olhada na representação dos vetores para entendermos melhor o problema:
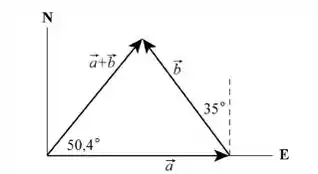
Temos que :
Consideremos . Sendo assim ,
O módulo de , portanto , é :
Passo 2
Podemos calcular o ângulo entre o vetor e o semieixo positivo através da relação:
A segunda possibilidade se mostra incoerente , porque o vetor apontaria no sentido contrário ao sentido do vetor .
Até aqui , beleza? Vamos para o próximo item então!
Passo 3
Agora bora dar uma olhada na representação do vetor :
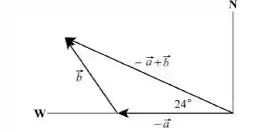
As suas componentes , portanto , são :
O módulo de pode ser obtido através da fórmula :
Passo 4
Bom pessoal , a tangente do ângulo que faz com o semieixo positivo vai ser dada por :
Com isso chegamos em duas soluções :
Como podemos perceber na representação do vetor , o ângulo correto é o , já que a orientação do vetor está aproximadamente ao norte do oeste .
Passo 5
Já desenhamos os diagramas vetoriais no decorrer da questão
Atenção! Cientistas afirmam que o próximo exercício tem 117,3% de chances de cair na sua prova , não deixem de conferir
Resposta
Ei, a resposta está no passo a passo :)