Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 3.6 - Ex. 17
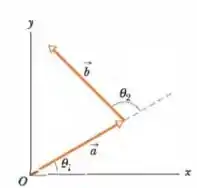
Os vetores e da Fig. 3-28 têm o mesmo módulo, , e os ângulos mostrados na figura são e . Determine as componentes (a) e (b) da soma vetorial dos dois vetores, (c) o módulo de e (d) o ângulo que faz com o semieixo positivo.
Passo 1
Como esta é uma questão de soma de vetores vamos iniciar decompondo os dois vetores dados em componentes.
Após escrever os vetores em função das componentes, vamos fazer a soma vetorial:
Em seguida, com o vetor resultante escrito em função das componentes, vamos aplicar a definição de módulo de vetor:
E, por fim, usaremos a trigonometria para determinar o ângulo que faz com o semieixo positivo.
Passo 2
Escrevendo o em função das componentes:
Substituindo os valores dados no enunciado:
Passo 3
Para escrever o vetor em função das componentes, vamos ilustrá-lo inidividualmente no plano cartesiano para podermos visualizar melhor o ângulo formado com o semieixo positivo de :
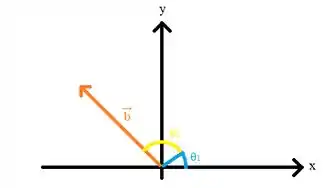
Com essa ilustração conseguimos perceber que o ângulo que o vetor faz com o semieixo positivo de é:
Substituindo os valores:
Portanto, escrevendo em função das componentes:
Substituindo os valores:
Passo 4
Com os valores das componentes dos vetores em mãos podemos fazer o somatório vetorial definido no passo , logo:
Passo 5
Agora, aplicando a definição de módulo de vetor, também anunciado no passo :
Passo 6
Para determinar o ângulo que o vetor faz com o semieixo positivo vamos representa-lo no plano cartesiano para conseguir visualizar melhor:
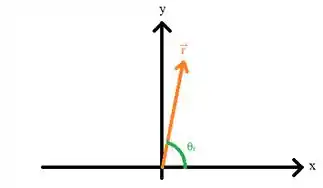
Tendo em mente que:
Isolando o cosseno:
Isolando o :
Substituindo os valores:
Resposta
- ;
- ;
- ;
- .