Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.8 - Ex. 41
Um professor de física desorientado dirige do sul para o norte, depois de leste para oeste e a seguir do norte para o sul. Determine o módulo, a direção e o sentido do deslocamento resultante, usando o método dos componentes. Usando diagramas (aproximadamente em escala), mostre que o deslocamento resultante encontrado em seu diagrama concorda aproximadamente com o resultado obtido pelo método dos componentes.
Passo 1
Faala ae, beleza??
Nesse tipo de questão é bem importante ler as informações uma a uma e observar como ficam os vetores deslocamentos. Uma rosa dos ventos também pode ajudar bastante.
Belezoca galerinha, analisando o problema temos que o professor fez três deslocamentos que vamos chamas de e . Além disso, sabemos a magnitude e a direção desses deslocamentos.
O problema pede para que encontremos a resultante desses deslocamentos, ou seja, a soma dos três deslocamentos.
Graficamente o vetor resultante é aquele que sai da origem do primeiro vetor, no caso o , e encontra o final do último vetor, que é o .
Vamos ilustrar esse deslocamento para visualizarmos melhor:
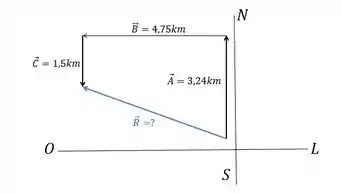
Veja só! 😉
Passo 2
Iradoso! Mas o problema pede pra gente fazer essa soma usando o método das componentes. Isso significa que vamos encontrar o vetor resultante em termos das componentes e de cada vetor.
Vamos fazer um de cada vez!!!
Para o eixo , somamos as componentes de cada deslocamento, sendo:
Mas, já que e só têm componente em (isso porque eles estão completamente na vertical). Então:
Só teremos a componente , e vemos que o vetor está totalmente na horizontal. Logo deve ter o tamanho do próprio vetor:
Isso é algo que podemos ver no diagrama do passo anterior.
Com isso teremos a primeira componente do nosso vetor resultante , sendo:
Como esse deslocamento foi no sentido negativo de :
Agora vamos ao deslocamento em :
Sabemos que só tem componente em . Então:
Já os outros dois vetores, só possuem a componente em e podemos dizer que essa componente deve ter o tamanho dos vetores completos. Então:
Como o deslocamento de foi no sentido negativo de :
Portanto, substituindo para achar , ficamos com:
Tranquilo até aqui? 😁
Passo 3
Show de bolinhas!
Como já conhecemos as componentes em e , o próximo passo é calcular o módulo para encontrar o vetor resultante .
Bacana, não é? 👀
Passo 4
Agora é hora de calcular a direção do vetor :
Para isso, vamos utilizar a relação:
E sabemos que:
Então:
Esse é o ângulo que o vetor faz com o eixo horizontal, ok?? Portanto, do Leste para o oeste.
Só isso! O que achou? Responde Aí! 😊
