α em relação ao plano horizontal, como demonstra a Figura 1.42. Seu peso exerce uma força sobre a pedra no sentido verticalmente para baixo. a) Em termos de e p, qual é o componente do peso da pedra na direção paralela à superfície da colina?

Vamos ilustrar com uma imagem:

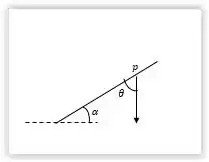
Pela imagem da pra perceber que o ângulo que o vetor peso faz com a superfície é oposto ao ângulo . Por conta disso temos as seguintes componentes para o vetor peso:

Sendo que está relacionada à componente paralela à colina e está relacionada à componente perpendicular à colina. Portanto a nossa resposta é .

Bora pra próxima!