Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo R.1 - Ex. 16

16. A vida média própria de um píon (uma partícula subatômica) é de 2,6 ∙ 10 - 8   s . ( Um píon neutro tem uma vida média bem mais curta). Um feixe de píons tem uma rapidez de 0,85 c em relação ao laboratório.

(a) Qual é a sua vida média medida no laboratório?

(b) Na média, qual é a distância percorrida por eles no laboratório antes de decair?

(c) Qual seria sua resposta para a parte (b) se você tivesse desprezado a dilatação temporal?

Passo 1

(a) O píon entra no laboratório em um ponto chamado de porta de entrada   ( E P ) . Um píon típico no feixe se desintegra em um segundo ponto chamado de local médio de desintegração ( M D L ) . Vamos chamar essas duas situações de eventos A e B , respectivamente; onde o evento A ocorre quando um típico píon entra na sala em E P , e o evento B ocorre quando o píon se desintegra no   M D L . Temos então que no quadro de referência da viga, esses dois eventos ocorrem no mesmo local, de modo que o tempo ∆ t 0   entre eles nesse referencial é o intervalo de tempo adequado. Baseado nisso, podemos usar a fórmula de dilatação do tempo para calcular o tempo ∆ t entre esses eventos no referencial do laboratório, o qual se move com velocidade v = 0,85 c   em relação ao ponto de referência do feixe.

Primeiramente, vamos esboçar um píon típico no quadro de referência do feixe. Nesse referencial, o píon típico está em descanso e ambos, E P   e M D L , estão movendo-se na velocidade v . O evento A ocorre quando o E P está próximo dofeixe de píons, e o evento B ocorre quando o MDL atinge o píon no instante em que este, desintegra-se:

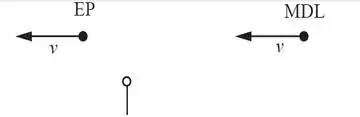
Agora, vamos esboçar um píon na referência do laboratório. Considerando que o píon se move em velocidade v , temos que o evento A ocorre quando um típico píon entra no referencial E P , e o evento B ocorre quando o píon atinge M D L no instante em que este desintegra-se:

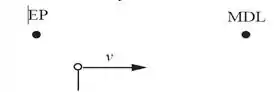
Bom! Chega de desenhinho! Porque agora, o que temos que fazer é usar a equação de dilatação do tempo para relacionar a vida útil média ∆ t do nosso píon na estrutura do laboratório para a vida útil média adequada ∆ t 0 no quadro de referência do feixe. Vamos aos cálculos:

∆ t = t 0 1 - v c 2

Substituem-se os valores numéricos adequados:

∆ t = 2,6 ∙ 10 - 8   s 1 - 0,85 c c 2

∆ t = 2,6 ∙ 10 - 8   s 1 - 0,85

∆ t = 2,6 ∙ 10 - 8   s 0,2775

∆ t = 4,935 ∙ 10 - 8   s

Passo 2

(b) Expresse a distância que o píon vai viajar na estrutura do laboratório antes que decaia de uma maneira típica. Isso mesmo se você pensou na fórmula do sorvete, acertou. A distância percorrida ∆ s , vai ser dada em termos da velocidade e sua vida média útil no laboratório:

∆ s = v ∆ t

Sustituindo os valores númericos convenientes, onde ∆ t é o intervalo de tempo lá da letra (a), encontramos que:

∆ s = ( 0,85 c   m / s ) ( 4,935 ∙ 10 - 8   s )

∆ s = ( 0,85 ∙ 2,998 ∙ 10 8     m / s ) ( 4,935 ∙ 10 - 8   s )

∆ s = 12,576   m

Passo 3

(c) Para esse item, como a própria questão diz, basta desprezar a dilatação temporal e usar a fórmula do sorvete ∆ s = v ∆ t   para encontrar a distância percorrida. Mas atenção, porque o tempo não se dilata mais. Logo, nosso ∆ t é a vida média útil adequada; dada por ∆ t 0   :

∆ s = v ∆ t 0  

∆ s = ( 0,85 c   m / s ) ( 2,6 ∙ 10 - 8   s )

∆ s = ( 0,85 ∙ 2,998 ∙ 10 8     m / s ) ( 2,6 ∙ 10 - 8   s )

∆ s = 6,625   m

Resposta

a) 4,935 ∙ 10 - 8   s  

b) 12,576   m

c) 6,625   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

20. Você recebeu a missão de monitorar o tráfego em uma região remota do espaço. No final de um turno tranquilo você mede, com um dispositivo a laser, o comprimento de uma nave espacial que está passa
23. Uma régua de um metro se move, na direção de seu comprimento, com uma rapidez de 0,80c em relação a você.(a) Determine o comprimento da régua, conforme medido por você.(b) Quanto tempo a régua lev
24. Lembre-se que a meia-vida é o tempo que leva para qualquer quantidade de partículas instáveis decair à metade de seu número inicial. A meia-vida própria de uma espécie de partículas subatômicas ca
22. A vida média de um feixe de partículas subatômicas chamadas de píons (Veja o problema 16 para detalhes sobre estas partículas), viajando com grande rapidez, é medida como 7,5 × 10 - 8s . Sabe-se q
21. Uma nave espacial viaja da Terra para uma estrela distante 95 anos-luz, com uma rapidez de 2,2× 10 8m / s . Quanto tempo a nave leva para chegar à estrela:(a) conforme medido na Terra?(b) conforme