Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 20.Problemas - Ex. 41
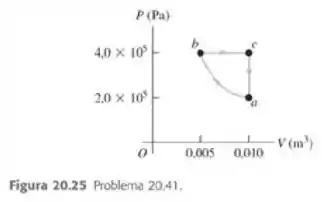
Você constrói uma máquina térmica que requer de um gás ideal diatômico em todo o ciclo mostrado na figura 20.25. a) Mostre que o segmento é uma compressão isotérmica. b) Durant qual(is) segmento(s) do ciclo o calor é absorvido pelo gás? Durante qual(is) segmento(s) o calor é rejeitado? Como você sabe disso? c) Calcule a temperatura nos pontos , e . d) Calcule o calor total trocado com o meio ambiente e o trabalho realizado pela máquina em um ciclo. Calcule a eficiência térmica da máquina.
Passo 1
a) Para mostrarmos que o processo é isotérmico, a gente supõe que ele é e usa a equação dos gases ideais para confirmar
E igualamos os estados e já que o lado direito é constante:
Se cada produto der o mesmo resultado, significa que podemos fazer a igualdade, e portanto, a temperatura é constante:
Como podemos ver, os valores são iguais, então o processo é isotérmico.
Passo 2
b) O processo é uma compressão, o que significa que o trabalho do gás é negativo, e pela primeira lei da termodinâmica:
A variação de energia interna será zero porque o processo é isotérmico, então:
Como a gente concluiu que o trabalho tem valor negativo por se tratar de uma compressão, o calor é negativo e tem o mesmo valor.
No processo o gás está a pressão constante, a equação de calor para esse caso é:
Substituindo usando a equação dos gases ideais:
Como o volume aumenta nesse processo, o valor da equação acima será positivo e o gás absorve calor.
E no último processo , o processo é dado a volume constante, então a equação de calor é:
Substituindo de novo :
Como a a pressão cai, o será negativo e o calor é liberado nesse processo.
Passo 3
c) Como a pressão e o volume de cada ponto é dado e o numero de mol é dado, basta usarmos a equação dos gases ideais para cada caso e isolar a temperatura:
Para o ponto :
Como o processo é isotérmico, se já temos a temperatura do ponto sabemos a do ponto :
E para o ponto :
Passo 4
d) O calor total trocado com o meio pela maquina é a soma do calor absorvido ou liberado por cada processo:
Para o processo podemos suar a equação:
Para os outros processos, vamos usar e que são os valores para um gás ideal diatômico. Calculando o calor de :
E para o calor de :
E a soma de todos é:
E o trabalho total terá o mesmo valor, já que no processo como havíamos dito no Passo 1 através da primeira lei da termodinâmica, o que significa que o trabalho será igual.
No processo o valor pode ser calculado por:
E no processo , como o volume não varia, .
Fazendo a soma:
Passo 5
e) A eficiência térmica é a razão entre o trabalho total e o calor absorvido pela máquina, que será o calor do processo , quando o gás expande: