Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 24.1 - Ex. 14
Você faz parte de uma equipe de pesquisa em engenharia que está projetando um laser pulsado de nitrogênio. Para criar as altas densidades de energia necessárias para operar este tipo de laser, é usada a descarga elétrica de um capacitor de alta tensão. Tipicamente a energia necessária por pulso (isto é, por descarga) é . Estime o valor da capacitância necessária se a descarga deve criar uma faísca através de um espaçamento de aproximadamente . Considere que o valor da tensão de ruptura dielétrica do nitrogênio é o mesmo que o do ar normal.
Passo 1
Cara... Imagina um relâmpago...
O relâmpago nada mais é do que a transferência de energia elétrica entre a nuvem e a terra quando a diferença de tensão entre esses dois é MUITO ALTA. Essa tensão é chamada de tensão de ruptura e ela tem esse nome, pois se você tiver aquela tensão ali, você pode tornar o ar condutor e fazer passar uma corrente elétrica gerando essa luminosidade!
“Tá, mas porque você está me falando isso?”
Por que o nosso problema é parecido, mas diferentemente do relâmpago, a gente só quer criar de faísca. A tensão de ruptura do ar é...
Isso significa que a cada de raio, você precisa adicionar . Como queremos apenas um de raio, precisamos ter nesse capacitor do problema uma tensão de ...
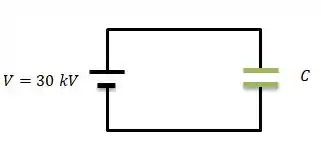
E com essa tensão ele precisa armazenar uma energia de . Então o problema é justamente determinar a capacitância , para que isso ocorra, saca?
Passo 2
Ora... Por sorte conhecemos uma expressão maravilhosa que nos fala que a energia armazenada em um capacitor vale...
Como queremos o valor da capacitância, basta isolar...
Substituindo e ou ainda ...
Como é aproximadamente , então...
Só que é o mesmo que ...
Saca? Então com essa capacitância, e a tensão de será possível armazenar a energia requerida no problema .