Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 5.Problemas - Ex. 1
Na experiência de Millikan, uma gota de óleo microscópica, de de raio, é introduzida entre placas de um capacitor plano, cujo espaçamento é de . A densidade do óleo é de . Com as placas inicialmente descarregadas, observa-se que a gota cai, atingindo, devido à resistência do ar, uma velocidade terminal . Quando se aplica entre as placas uma diferença de potencial de , com o campo elétrico orientado para cima, verifica-se que a velocidade de queda duplica. Qual é o sinal e o valor da carga, em unidades de carga elétron?
Passo 1
Se liga, no enunciado diz que a partícula cai com o capacitor descarregado atingindo uma velocidade terminal e, quando o capacitor se carrega, o campo elétrico fica orientado para cima e a velocidade terminal da partícula atinge . Vamos montar nosso desenho para o capacitor descarregado e para ele carregado. Beleza?
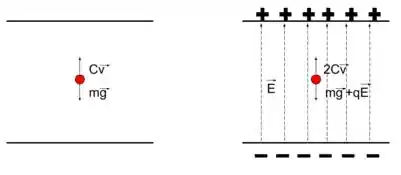
Pelas leis de Newton podemos escrever para o capacitor descarregado
e para ele carregado
Passo 2
Precisamos substituir a expressão de na segunda equação
Daí teremos
Passo 3
Ele não nos forneceu a massa e nem o campo elétrico, mas sabemos que
Sendo assim, podemos escrever que
onde é o potencial dado de , é , é o volume do cubo de raio , é a gravidade e é a distância entre os terminais do capacitor .
Agora só precisamos substituir os valores na equação (prestando atenção nas unidades, né?!)
Passo 4
Como a partícula se orienta no sentido contrário ao campo, podemos dizer que ela é negativa!