Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 3- Ed: 1º - Capítulo 5.Problemas - Ex. 2

Dois capacitores, de capacitâncias C e 2 C , estão carregados com a mesma carga Q e inicialmente isolados um do outro. Se as placas negativas de ambos forem ligadas à terra e as positivas ligadas uma à outra,

  1. Qual será o potencial final das placas positivas?
  2. Qual é a variação de energia neste processo?
  3. O que acontece com essa energia?

Passo 1

Inicialmente temos

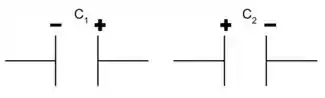
A carga depositada e a diferença de potencial em C 1 é Q 1 e V 1 , já para C 2 é Q 2 e V 2 , respectivamente.

Depois que ligamos as placas negativas à terra e os ligamos um ao outro pela placa positiva, temos

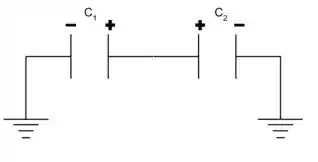
Agora a carga depositada e a diferença de potencial em C 1 e C 2 passa a ser ( Q ' 1 , V ' 1 ) e ( Q ' 2 , V ' 2 ) , respectivamente.

Passo 2

Pela conservação da carga podemos escrever que

Q 1 + Q 2 = Q ' 1 + Q ' 2

Lembrando que Q = C V , temos

C 1 V 1 + C 2 V 2 = C 1 V ' 1 + C 2 V ' 2

Substituindo os valores da Capacitância de cada capacitor, lembrando que os mesmos estão carregados com carga Q e que quando aterrados passam a estar submetidos a mesma diferença de potencial, temos

2 Q = C + 2 C V

⇒ V = 2 Q 3 C

Essa é a resposta do item (a). Partiu para a próxima?

Passo 3

Para o item (b), precisamos lembrar que a energia é dada por

U = 1 2 C V 2

Assim, temos no final uma energia

U f = 1 2 3 C 4 Q 2 9 C 2 = 2 Q 2 3 C

No início as energias são

U 1 = 1 2 C Q 2 C 2 = Q 2 2 C

U 2 = 1 2 2 C Q 2 4 C 2 = Q 2 4 C

Agora é só lembrar que

Δ U = U f - U i

Δ U = 2 Q 2 3 C - Q 2 2 C - Q 2 4 C = - Q 2 12 C

Mas, se tratando apenas da variação, podemos olhar para o módulo dessa variação também:

∆ U = Q 2 12 C

Passo 4

Parte da energia é perdida, podendo esta ter sido convertida em outras formas.

Resposta

a )           V = 2 Q 3 C

b )       ∆ U = Q 2 12 C

c )           P a r t e   d a   e n e r g i a   é   p e r d i d a ,   p o d e n d o   e s t a   t e r   s i d o   c o n v e r t i d a   e m   o u t r a s   f o r m a s .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um capacitor de placas pararelas está imerso no ar, cuja rigidez vale 3 k V / m m . (A) Mostre que a energia potencial máxima que pode ser acumulada no capacitor somente depende do volume do espaço in
Calcule:a) a capacitância de um par de placas paralelas com área de 100c m 2 cada, separadas de 3,0m m ;b) o campo elétrico quando o capacitor possui uma carga de 0,10μ C .
Calcule:a) a capacitância de uma esfera metálica de 1,0c m de raio;b) a energia de seu campo se a esfera está a um potencial de 100V em relação ao infinito.
As duas placas de um capacitor esférico têm raios de 5,0c m e 10,0c m . Calcule:a) a sua capacitância;b) o campo elétrico em pontos equidistantes das duas placas, quando o capacitor tem carga de 1,0μ
Um capacitor de placas paralelas, de capacitância igual a 200p F e placas separadas de 1,00m m , tem uma diferença de potencial de 50V entre as placas. Calcule a força entre as placas.