Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 8.Problemas - Ex. 101
Você está em pé sobre um bloco de concreto apoiado sobre um lago congelado. Suponha que não exista atrito entre o bloco e a superfície do lago congelado. Você possui um peso cinco vezes menor do que o peso do bloco. Se você caminhar para frente com velocidade de , com que velocidade o bloco se moverá em relação ao gelo?
Passo 1
Fala, galerinha! Beleza? Vamos resolver essa questão!
O enunciado nos dá uma situação de uma pessoa em cima de um bloco em contato com o solo (de gelo), onde é desconsiderado o atrito. Para resolver esse problema iremos usar conservação de momento, onde iremos comparar os momentos iniciais e finais para descobrir a velocidade do bloco que irá se deslocar.
Mas vamos entender melhor o que está acontecendo!
Pensa que você está em pé sobre o bloco, sem se movimentar. Dessa forma, o bloco também permanece parado, ok? Após isso, você decide andar sobre o bloco, o que gera um movimento contrário do bloco, já que passaram a ter forças agindo no sistema, como podemos ver na imagem abaixo:
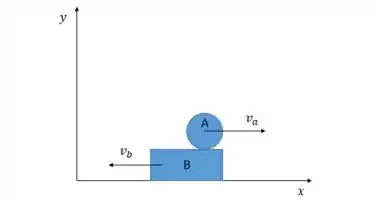
Agora vamos resolver essa questão!
Passo 2
Note que há forças externas atuantes, logo o momento se conservará e poderemos aplicar a relação de conservação:
Como o momento é dado pelo produto entre a massa e a velocidade, temos:
Onde é a velocidade do centro de massa inicial, é a velocidade da pessoa e é a velocidade do bloco. Como o sistema inicialmente está em repouso, logo seu centro de massa também não está se movendo. Portanto,
Assim, temos que o momento ficará:
E, isolando o :
Como você possui um peso 5 vezes menor que o bloco, sua massa também será,
Logo:
Esse sinal negativo só nos indica o sentido adotado!
Portanto, o bloco se moverá para a esquerda com uma velocidade de .
Valeu, galera! Até a próxima! 😉