Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 8.Problemas - Ex. 88

Um disco de hóquei azul de massa 0,0400   k g , deslizando com velocidade igual a 0,200   m / s sobre uma mesa de ar horizontal sem atrito, sofre uma colisão frontal perfeitamente elástica com um disco de hóquei vermelho de massa m , inicialmente em repouso. Depois da colisão, a velocidade do disco de hóquei azul é de 0,050   m / s no mesmo sentido da sua velocidade inicial. Determine

a) o módulo, a direção e o sentido do disco de hóquei vermelho depois da colisão

b) a massa m do disco de hóquei vermelho.

Passo 1

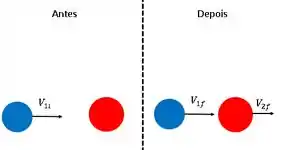
No inici do nosso problemas temos o disco azul se aproximando no disco vermelho de massa m . Posteriormente ao choque elástico, temos o disco azul se movendo na mesma direção, mas agora com uma velocidade menor. Consequentemente a isso, temos o disco vermelho também produziu uma quantidade de movimento.

Passo 2

  1. Pela E q . ( 8.27 ) temos que, em colisões perfeitamente elásticas,

    2. v 2 f x = v 1 f x - v 2 i x + v 1 i x

    Assim temos que o disco vermelhor partiu do repouso, ou seja, v 2 i x = 0 , desta forma

    v 2 f x = 0,2 m s + 0 + 0 m s +   0,05 m s = 0,25 m s

    Passo 3

  2. Usando o princípio da conservação de momento, temos que

m 1 v 1 i + m 2 v 2 i = m 1 v 1 f + m 2 v 2 f

Ou seja, a quantidade de movimento de todos os disco no inicio deve ser iqual a quantidade de movimento dos discos ao final.

Como o disco vermelho parte do repouso, temos que v 2 i = 0 . Assim ficamos apenas com

( 0,04 k g ) ⋅ 0,2 m s = 0,04 k g ⋅ 0,05   m s   + m 2 ⋅ ( 0,25   m s   )

Isolando m 2 , temos

m 2 = 0,04 k g ⋅ 0,2 m s - 0,05 m s   0,25   m s = 0,024 k g  

Resposta

  1. v 2 f =   0,25 m s  
  2. m 2 = 0,024 k g
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois flutuadores planadores são colocados em movimento em um trilho de ar horizontal. Uma mola de constante de força k é presa à extremidade traseira do segundo planador flutuador. Como mostrado na Fi
Duas partículas com massas m e 3 m estão se movendo uma em direção à outra ao longo do eixo x com a mesma velocidade inicialv i . A partícula m está indo para a esquerda e a 3 m , para a direita. Elas
8.6P Resolva o problema da colisão entre uma nave e um planeta, tratado na Seção 8.5, o referencial em que a nave está parada. Nesse caso, você estará usando o segundo limite da colisão, ou seja, a pa
8.7P Uma molécula de oxigênio O 2 , inicialmente à velocidade 1000m/s , colide frontalmente com outra molécula de oxigênio parada. Antes da colisão, uma das moléculas estava em um estado de vibração,
8.5P Uma bola de massa m e velocidade v colide frontalmente com outra bola de massa M . Na colisão, uma fração f de energia mecânica do sistema é transformada em calor. Calcule ás velocidade finais da