Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 9.7 - Ex. 43
A Fig. 9-55 mostra um “foguete” de duas pontas que está inicialmente em repouso em uma superfície sem atrito, com o centro na origem de um eixo . O foguete é formado por um bloco central (de massa ) e dois blocos e (de massa cada um) dos lados esquerdo e direito. Pequenas explosões podem arremessar esses blocos para longe do bloco , ao longo do eixo . Considere a seguinte sequência: (1) No instante , o bloco é arremessado para a esquerda com uma velocidade de em relação à velocidade que a explosão imprime ao resto do foguete. (2) No instante , o bloco é arremessado para a direita com uma velocidade de em relação à velocidade do bloco nesse momento. No instante , quais são (a) a velocidade do bloco e (b) a posição do centro do bloco ?
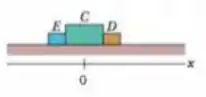
Passo 1
Analisando o primeiro instante, vamos considerar que o sistema formado pelas partes e se movem com uma velocidade para direita. Assim, a velocidade da parte será . Lembrando que como foi uma explosão interna, podemos aplicar a lei da conservação do momento linear, assim:
Isolando :
Substituindo os valores:
Passo 2
Analisando agora o instante , instante em que ocorre a segunda explosão, podemos aplicar novamente a lei da conservação da energia, porém, usaremos apenas as partes que estão envolvidas nessa segunda explosão ( e ). Isso nos dá que:
Isolando :
Substituindo os valores, temos:
Portanto, a velocidade do bloco , após a segunda explosão é:
Passo 3
Para determinar a posição do bloco , devemos perceber que entre os instantes e , o bloco possui uma velocidade de e, após a segunda explosão, ele passa a se locomover a uma velocidade de . Ambos os movimentos são uniformes, portanto, vamos calcular a distância de cada trecho separadamente. De até :
De até :
Portanto, a posição de no instante é .
Resposta
- ;