Você está projetando um elevador para um hospital. A força exercida sobre um passageiro pelo piso do elevador não deve exceder a o peso do passageiro. O elevador acelera de baixo para cima com aceleração constante por uma distância de e depois começa a reduzir a velocidade. Qual é a velocidade escalar máxima do elevador?

Bom... O descritivo do problema é um elevador que sobe e depois tem sua velocidade reduzida. Então bora entender as forças envolvidas aqui!

Primeiro passo é desenharmos um diagrama de corpo livre da situação, então temos que:

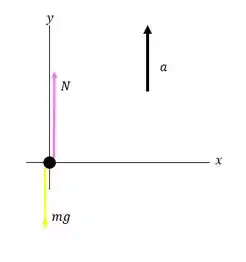
Agora vamos aplicar a segunda lei de Newton ao passageiro para encontrarmos a aceleração máxima permitida.

Nessa questão, precisaremos usar a equação de aceleração para encontrar a velocidade máxima.

Como o novo movimento é na vertical somente, temos pela segunda lei de Newton:

E isso nos dá que:

Onde é a força normal, é a massa do massageiro e é a aceleração da gravidade.

Como a força exercida sobre um passageiro pelo piso do elevador não deve exceder a o peso do passageiro, temos:

Substituindo,

Simplificando,

Agora que temos a aceleração, vamos achar a velocidade!

Como não nos foi forneceido o tempo, podemos utilizar a equação de Torricelli:

Onde é a velocidade final é a velocidade inicial e é a altura.

E nós temos que

Substituindo na equação,

Uma velocidade final maior exigiria um valor maior de , o que significaria uma força normal maior sobre a pessoa.