Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 28.1 - Ex. 50

Voce recebe um fio de comprimentoe raio a e deve transforma-lo em um indutor enrolando-o na forma de uma helice com secao circular de raio r.As voltas devem estar o mais proximas possivel sem sobreposicao entre elas.Mostre que a auto-indutancia deste indutoreL=port/a.

Passo 1

E aí galera, vamos para a resolução de mais um exercício!!

O fio de comprimento l   e raio a   é mostrado no diagrama, assim como o indutor construído com este fio e cuja indutância L   deve ser encontrada. Podemos usar a equação para a auto-indutância de um indutor cilíndrico para derivar uma expressão para L .

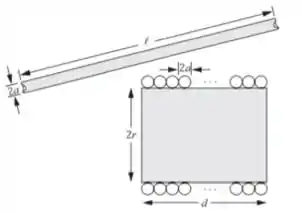
Passo 2

A auto-indutância de um indutância com comprimento d ,   área de seção transversal A e número de espiras por unidade de comprimento n   é:

L = μ 0 n 2 A d                                       ( 1 )

O número de espiras N   é dado por:

N = d 2 a ⇒ n = N d = 1 2 a

Supondo que a < < r , o comprimento do fio l está relacionado a N e r :

l = N ( 2 π r ) = d 2 a 2 π r = π r a d

Passo 3

Resolvendo para d , temos:

d = a l π r

Substitua por d ,   A e n na equação ( 1 ) para obter:

L = μ 0 1 2 a 2 π r 2 a l π r = 1 4 μ 0 r l / a

Resposta

Ver resolução

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A bobina 1 tem L 1 = 25m H e N 1 = 100 espiras. A bobina 2 tem L 2 = 40m H e N 2 = 200 espiras. As bobinas são mantidas fixas no espaço; a indutância múta é 3,0m H . Uma corrente de 6,0m A na bobina 1
Uma bobina retangular com N espiras compactas é colocada nas proximidades de um fio retilíneo longo, como mostra a figura 30-66. Qual é a indutância mútua M da combinação fio-bobina para N = 100 ,a =
Duas bobinas são mantidas fixas no espaço. Quando a corrente na bobina 1 é zero e a corrente na bobina 2 aumenta à taxa de 15,0A / s , a força eletromotriz na bobina 1 é 25,0m V . (a) Qual é a indutân
As duas bobinas da figura 30-68 têm indutâncias L 1 e L 2 quando estão muito afastadas. A indutância mútua é M . (a) Mostre que a combinação que aparece na figura pode ser substituida por uma indutânc
A bobina 1 tem L 1 = 25m H e N 1 = 100 espiras. A bobina 2 tem L 2 = 40m H e N 2 = 200 espiras. As bobinas são mantidas fixas no espaço; a indutância múta é 3,0m H . Uma corrente de 6,0m A na bobina 1