Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 33.1 - Ex. 49
Determine a resultante de duas ondas cujos campos elétricos em uma dada posição variam com o tempo como se segue: e .
Passo 1
Olá pessoal, tudo certo com vocês? Espero que sim 😊. Vamos entender melhor essa questão?
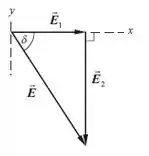
Certo! Observe que, escolhendo o sistema de coordenadas mostrado no diagrama de fases. Podemos usar os métodos padrão de adição vetorial para encontrar o resultado das duas ondas.
Passo 2
Certo, observe que o resultado das duas ondas é da forma:
Assim a magnitude de é:
E o ângulo é:
Substituindo o ângulo e a magnitude na equação das ondas, temos que
Passo 3
Pronto! Finalizamos a questão 😊. Nos vemos na próxima questão. OK? Até mais.
Resposta
Exercícios de Livros Relacionados
Determine a resultante de duas ondas cujos campos elétricos em uma dada posição variam com o tempo como se segue: 4 A 0 =E 1 →4 , 0s e nw t i ^ e 3 A 0 =E 2 →3 , 0s e n( w t + 1 6 π ) i ^ .
Luz monocromática incide em uma lâmina que contém uma fenda longa e estreita (Figura 33-45). Seja I 0 a intensidade no máximo central do padrão de difração em um anteparo distante, e seja I a intensid
Três fendas, cada uma separada da fenda ao lado por 60,0μ m , são iluminadas no máximo central de intensidade por uma fonte de luz coerente com comprimento de onda igual a 550n m . As fendas são extre
Luz monocromática incide em uma lâmina que tem três fendas longas, estreitas e igualmente espaçadas por uma distância d . (a) Mostre que as posições dos mínimos de interferência em um anteparo a uma g