Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 24.1 - Ex. 71
Você recebeu quatro capacitores idênticos e uma bateria de . Quando apenas um dos capacitores está conectado à bateria, a energia armazenada é . Combine os quatros capacitores de maneira tal que a energia total armazenada em todos os quatro capacitores é . Descreva a combinação e explique sua resposta.
Passo 1
Falaa galera, tudo bom? Essa questão trata sobre energia nos capacitores! Sabemos que existem diversas maneiras de se calcular a energia em um capacitor:
onde é a capacitância, a carga no capacitor e a voltagem em que ele está sujeito. É importante salientar que todas essas maneiras são equivalentes. Em especial, veja que
Passo 2
Sabemos que quando um capacitor é colocado no circuito, sua energia é . Assim,
Quando conectamos os 4, temos
onde é a capacitância equivalente do circuito. Igualando essas expressões, vemos que
Assim, devemos montar um circuito em que a capacitância equivalente seja igual a capacitância de um só capacitor. Uma das maneiras de fazer isso é mostrado abaixo.
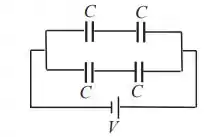
Notemos que temos dois conjuntos de capacitores ligado em série; cada conjunto terá uma capacitância equivalente . Assim, o circuito terá uma capacitância .
Resposta
Veja a figura.