Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 8.Exercícios e Problemas - Ex. 42
Você tem um novo emprego como projetista de brinquedo para um parque de diversões. Em um dos brinquedos, a cadeira do passageiro é presa por uma corrente de de comprimento ao topo de uma torre capaz de girar. A torre gira a cadeira e o passageiro a uma taxa de a cada . Em seu projeto, você supõe que a massa máxima conjunta da cadeira e do passageiro seja de . Você encontrou cadeiras por um preço bom em uma loja local que está fazendo promoções, mas seu supervisor fica preocupado se elas serão suficientemente resistentes. Você entra em contato com o fabricante e descobre que a cadeira foi projetada para resistir a uma tensão de até . A cadeira será resistente o suficiente para ser usada no brinquedo?
Passo 1
Olá, tudo bem?
Os dados que o problema nos dá são:
Vamos começar fazendo um desenho da situação.
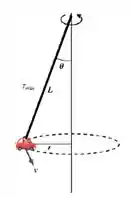
Para que seja suficiente, precisamos ver se quando a torre estiver girando, a tensão será suficiente, ou seja, se ela será maior ou menor que a força centrípeta que ocorre no movimento.
Pelo desenho vemos que na direção radial temos a força centrípeta e a componente horizontal a tensão. Tomando como o ângulo de referência, essa componente da tensão será . Assim da segunda lei temos:
Passo 2
Agora vamos olhar novamente o desenho, agora com mais carinho. Em relação ao ângulo , o raio da trajetória fica sendo o cateto oposto e o comprimento da corrente a hipotenusa, então , e com isso podemos substituir na expressão para a tensão ali do passo anterior e por fim determinar a tensão:
Lembrando que a velocidade é dada por , então:
Agora, comparando a tensão que achamos com lá do começo dessa resolução, temos:
Então, concluímos que a corrente não é suficiente para suportar a cadeira.
Beleza?
Espero ter ajudado!
Vamos pra próxima?