Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 8.Exercícios e Problemas - Ex. 51
Um bloco de aço de 500 g descreve um círculo preso por uma haste de peso desprezível com de comprimento. Ar comprimido é introduzido pela haste e injetado por um bico na parte traseira do bloco, exercendo sobre ele uma força de empuxo de . O bico está orientado a da linha radial, como mostra a FIGURA . O bloco parte do repouso.
a. Qual é a velocidade angular do bloco após revoluções?
b. Quanto vale a tensão na haste após revoluções?
Passo 1
Olá, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?
Os dados que o problema nos dá são os seguintes:
O ângulo da velocidade tangencial com a horizontal vale , pois . Saca só nesse desenho:
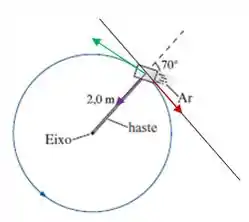
A força de empuxo está representada em verde, a força de atrito em vermelho e a centrípeta em roxo. O ângulo que a força de empuxo faz com a horizontal é de . Ainda temos duas outras forças: a força peso e a normal. Elas se cancelam (), pois não temos movimento na vertical. Vou chamar de a tensão na haste.
Na direção radial temos que a resultante é a força centrípeta, já na direção perpendicular a ela, ou seja, ao longo do eixo que tangencia a circunferência, temos equilíbrio de forças. Assim conseguimos formar o seguinte sistema de equações:
Passo 2
Letra a)
Agora, da segunda equação temos:
O deslocamento angular foi de , ou seja, , então o tempo transcorrido, considerando e , foi:
E agora podemos calcular a velocidade angular, já que temos o tempo e a aceleração:
Passo 3
Letra b)
Agora queremos determinar a tensão. Dá uma espiadela no nosso sistema de equações e resgata de lá a primeira delas:
Aqui propositalmente coloquei a força centrípeta em termos da velocidade angular =D
Usando os dados do problema junto com a velocidade angular calculada no passo anterior, é só substituir ali em cima para achar a tensão:
Beleza?
Espero ter ajudado!
Vamos pra próxima?