Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 77

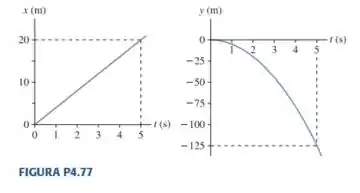
Escreva um problema realista para o qual os gráficos e mostrados na FIGURA P4.77 representem movimento de um objeto. Tenha certeza de que sua resposta seja consistente com os gráficos. Depois resolva o problema proposto.

Passo 1

O primeiro gráfico a função em relação a é uma reta crescente, o que significa que a equação que descreve esse gráfico é:

Ou seja, a velocidade do movimento do corpo é constante no eixo , e como ela passa pelo zero, isso significa que .

Para o outro gráfico, a função é uma parábola com concavidade voltada para baixo com o vértice em , significa que depende quadraticamente de , a equação será do tipo:

Mas como o vértice está em zero, isso significa que , e , e como a concavidade é voltada para baixo, é uma constante negativa.

Passo 2

Podemos dizer que esse movimento é o lançamento de um projétil de uma altura qualquer, sendo que esse projétil só tende a cair, sem subir nenhuma unidade em no inicio do lançamento, já que começa em e depois só decresce (se o projetil subisse um pouco antes de começar a cair, o lançamento teria um ângulo com a horizontal, mas nesse caso ele é ).

O problema pode ser o seguinte: Um canhão atira uma bala do alto de uma muralha com altura de , o ângulo que o canhão forma com a horizontal é , após um intervalo de tempo, a bala atinge o solo em , calcule a velocidade inicial do movimento da bala considerando que a posição da muralha está em . (Considere também que a posição inicial da bala é .)

Passo 3

Repare que o problema que escrevemos no Passo 2 não deu o valor do tempo que a bala leva para cair, e nos pede que é a posição da bala em relação à muralha, então precisaremos desse tempo.

Vamos começar usando a equação para o eixo :

A posição inicial da bala deve ser zero segundo a questão, então a final deve ser , além disso, como dissemos no passo 1, o único termo que não é zero, é o que envolve , já que o vértice da parábola está no . Isso significa que

O que está de acordo com o problema, já que o ângulo e então .

A equação então fica:

Isolando :

Passo 4

Agora usamos a equação para o movimento no eixo , como a aceleração é :

Sabemos que , o que significa que:

Toda a velocidade inicial aponta na direção . Como , ficamos com:

Isolando a velocidade:

Substituindo e o valor dado de :

A velocidade da bala vai ser:

Essa vai ser a solução do nosso problema que criamos que condiz com os gráficos do enunciado. (Poderíamos ter usado , para que os valores fiquem exatamente iguais aos dos gráficos.)