Você utiliza um fio longo e fino para montar um pêndulo em uma feira de ciências. O fio tem um comprimento não esticado de 22,0 m e uma seção reta com diâmetro de 0,860 mm; ele é feito de uma liga com uma grande tensão de ruptura. Uma extremidade do fio será presa ao teto, e uma esfera metálica de 9,50 kg será presa à outra extremidade. À medida que o pêndulo balança, o deslocamento angular máximo do fio a partir da vertical será de 36,0°. Você precisa determinar o tamanho máximo que o fio esticará durante esse movimento. Assim, antes de prender a esfera metálica, você suspende uma massa de teste (massa m) pela ponta inferior do fio. Então você mede o aumento no comprimento l do fio para diversas massas de teste diferentes. A Figura P11.86, um gráfico de l em função de m, mostra os resultados e a linha reta que oferece o melhor ajuste aos dados. A equação para essa linha é l (0,422 mm/kg)m. (a) Suponha que g 9,80 m/s2 e use a Figura P11.86 para calcular o módulo de Young Y para esse fio. (b) Você remove as massas de teste, prende a esfera de 9,50 kg e solta a esfera do repouso, com o fio deslocado por 36,0°. Calcule a quantidade que o fio esticará enquanto balança pela vertical. Ignore a resistência do ar

Como

Usando a Conservação de Energia encontre a velocidade angular na posição 2 da esfera.

Tome a posição 2 como o nível de energia potencial gravitacional zero.

(sem perda de energia)

Então,

Letra b:

Abaixo, um diagrama para ilustrar melhor:

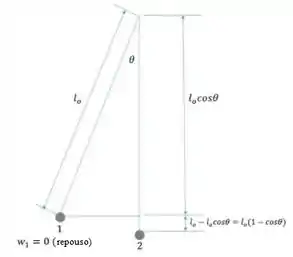
Em seguida, podemos fazer um diagrama de corpo livre da esfera para analisarmos quando o fio está na posição vertical.

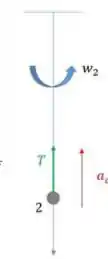
T é a força exercida sobre a esfera pelo fio. Pela 3ª Lei de Newton ele tem a mesma magnitude e direção oposta da força exercida pela esfera no fio. O fio está tenso.

Como F = T,