Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 38.Problemas adicionais - Ex. 85

Por volta de 1916, R. A. Millikan obteve os seguintes dados para o potencial de corte do lítio em experimentos do efeito fotoelétrico:

Use os dados da tabela para fazer um gráfico como o da Fig. 38-2 (que é para o sódio) e use o gráfico para determinar (a) a constante de Planck; (b) a função trabalho do lítio.

Passo 1

(a) A tabela deu valores de comprimento de onda, mas o gráfico que o enunciado pede para a gente fazer baseado na figura, está usando frequências, vamos então converter cada valor na tabela usando a equação da velocidade da luz no vácuo:

c = λ f

Ficamos com os seguintes valores de frequências para cada valor da tabela:

λ = 433,9 → f = 6,91 × 10 14   s

λ = 4 04 , 7 → f = 7,41 × 10 14   s

λ = 365,0 → f = 8,22 × 10 14   s

λ = 312,5 → f = 9,60 × 10 14   s

λ = 253,5 → f = 11,83 × 10 14   s

Passo 2

Com esses valores podemos fazer o gráfico:

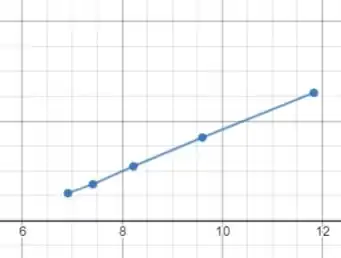
Onde o eixo das abscissas foi multiplicado por 10 14 .

A reta no gráfico terá uma inclinação de aproximadamente 4,14 × 10 - 15   V ⋅ s pelo método dos mínimos quadrados, multiplicada por e , que é a carga dos elétrons no experimento de efeito fotoelétrico a gente tem o valor 4,14 × 10 - 15   e V ⋅ s . Que o mesmo valor da constante de Planck.

Passo 3

(b) O método também dá o coeficiente linear da reta que é o ponto em que a reta cruza o eixo y e não está expresso no gráfico. Esse ponto corresponde ao negativo da função trabalho, ele será:

Φ = 2,31   e V

Resposta

a   4,14 × 10 - 15   e V ⋅ s  

b   Φ = 2,31   e V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

38.12. A função trabalho para o efeito fotoelétrico em uma superfície de potássio é 2,3 eV. Se uma luz com comprimento de onda igual a 250 nm incide sobre o potássio, calcule qual é a) o potencial de
38.13. Quando um feixe de luz ultravioleta de 254 nm incide sobre uma superfície polida de cobre, o potencial de corte necessário para impedir a emissão de fotoelétrons é igual a 0,181 V. a) Qual é o
38.8. Qual seria a função trabalho mínima que um metal deveria ter para que a luz visível (400-700 nm) emitisse fotoelétrons?
38.7. Uma superfície polida de níquel é exposta a um feixe de luz com comprimento de onda igual a 235 nm. Qual é a velocidade máxima dos fotoelétrons emitidos por essa superfície? Use a Tabela 38.1.
38.9. Uma fonte de luz de 75 W consome 75 W de potência elétrica. Suponha que toda essa energia se transfira para a luz emitida com comprimento de onda 600 nm. a) Calcule a frequência da luz emitida.