Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 3.Problemas - Ex. 53
Um avião bombardeiro da Segunda Guerra Mundial voa horizontalmente sobre terreno plano com velocidade de 275 m/s em relação ao solo e a uma altitude de 3,00 km. O bombardeiro solta uma bomba.
a. Que distância a bomba percorre horizontalmente entre sua liberação e seu impacto no solo? Ignore os efeitos da resistência do ar.
b. O piloto mantém o curso, a altitude e a velocidade originais do avião durante um ataque de fogo antiaéreo. Onde está o avião quando a bomba atinge o solo?
c. A bomba atinge o alvo visto pelo telescópio de mira do bombardeio no momento da liberação da bomba. A que ângulo da vertical a mira do bombardeio foi fixada?
Passo 1
a.Aqui é tranquilinho!
Como os deslocamentos horizontais de objetos em queda livre são movimentos uniformes (sem aceleração, a velocidade constante), vale a seguinte expressão pra distância , que queremos calcular:
Onde e são respectivamente a velocidade do deslocamento horizontal do objeto e o tempo demorado na queda.
Como o avião já se deslocava paralelamente ao solo, a velocidade do deslocamento horizontal dele, tanto como da bomba, é equivalente à velocidade dada no enunciado. Portanto vale que .
Com isso, até então, a gente tem:
Beleza! Pra gente finalmente determinar , vamos precisar determinar antes o valor de .
Passo 2
E determinar é tranquilo!
Visto de exercícios anteriores aqui no capítulo, a formulinha clássica que correlaciona o tempo de queda de um objeto (em queda livre) e a altura da qual ele parte é:
Onde vai valer ; , a aceleração da gravidade, vamos considerar como . Assim, a gente determina facinho!
Vamos ter:
Obtido o tempo , a gente retoma a última expressão do Passo 1 e determina a distância , tendo assim:
Passo 3
b.Como a gente considerou desprezível o efeito da resistência do ar, o avião vai, necessariamente, estar exatamente em cima do ponto onde a bomba atingiu o solo, ou seja, a do local onde liberou a bomba!
Passo 4
c.Nossa situação é mais ou menos essa:
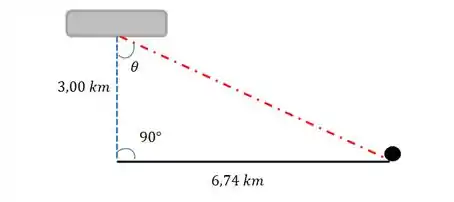
O avião, representado pelo retângulo cinza, precisou determinar o ângulo com a vertical pra saber quando realizar a soltura da bomba. Esse ângulo, calculado, possibilitou que a bomba caísse a exatos 6,74 quilômetros da posição de onde o avião a soltou, de modo estratégico.
A gente tem dados pra calcular a tangente desse ângulo , a partir dos catetos do triângulo retângulo formado entre a distância vertical avião-solo e a distância horizontal bomba-posição inicial.
Podemos escrever que:
Com isso, esse ângulo vai valer:
Resposta
a.
b. Vide Passo 3
c.