Duas rodovias se cruzam, como mostra a Fig. 4-46. No instante indicado, um carro de polícia está a uma distância do cruzamento, movendo-se com uma velocidade escalar . O motorista está a uma distância do cruzamento, movendo-se com uma velocidade escalar . (a) Qual é a velocidade do motorista em relação ao carro da polícia na notação de vetores unitários? (b) No instante mostrado na Fig.4-46, qual é o ângulo entre a velocidade calculada no item (a) e a reta que liga os dois carros? (c) Se os carros mantêm a velocidade, as respostas dos itens (a) e (b) mudam quando os carros se aproximam da interseção ?
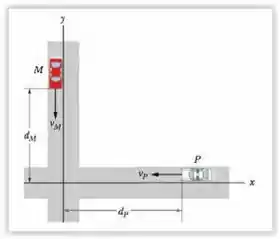
Passo 1
Bom pessoal , é sempre importante separarmos cada componente da questão por índices diferentes para visualizarmos melhor o problema , Beleza ? Usamos os índices e para designar o policial e o motorista. A velocidade do motorista em relação ao policial é :
Passo 2
tem a mesma direção que a reta que liga os dois carros. Observando a Fig. 4-46, vemos que o vetor que aponta de um carro para o outro é :
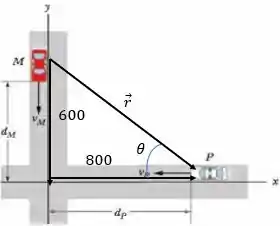
Como a razão entre os componentes de é a mesma que entre os componentes de :
Podemos afirmar que os dois vetores têm a mesma direção. Logo, o ângulo entre eles é zero.
Passo 3
Podemos reparar que a velocidade deles não se altera com o tempo. Logo, eles sempre vão se aproximar com a mesma velocidade... Além disso, a posição deles vai variar na mesma proporção ao longo do trajeto. Então, mantendo a velocidade, nada muda no problema.
Dessa forma, como nenhum fator de relevância para os 2 itens anteriores foi alterado, podemos concluir que as respostas permanecem as mesmas.
Tranquilo galera??? Bora resolver mais questões então!!!!
Resposta
(a)
(b)
(c) Nada muda